Tính cạnh của tam giác ABC đều biết diện tích của ABC là \(121\sqrt{3}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
a) Diện tích tam giác ABC = 1/2 x AH x BC
Diện tích tam giác ABE = 1/2 x AH x BE
= 1/2 x AH x 2/3 BC
= 1/2 x AH x BC x 2/3
= Diện tích tam giác ABC x 2/3
Vậy: Diện tích tam giác ABE = 2/3 diện tích tam giác ABC.
b) Vì chiều cao DE có D là trung điểm nên Diện tích tam giác ABE = 2 lần diện tích tam giác BDE
= 12 x 2
= 24
Diện tích tam giác ABC = 24 : 2/3
= 36
c) Diện tích hình tứ giác ADEC là: 36 - 24 = 12 ( cm vuông)
Đáp số: ...........................

Gọi cạnh tam giác là a
=> h =a\(\sqrt{3}\)/2
=> S =ah/2 = 121\(\sqrt{3}\)
=> a.a\(\sqrt{3}\)/2 = 121\(\sqrt{3}\)
=> a2 = 2.121
=> a =11\(\sqrt{2}\)

a: Xét ΔCAB có \(cosC=\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}\)
=>\(\dfrac{2^2+3-AB^2}{2\cdot2\cdot\sqrt{3}}=cos30=\dfrac{\sqrt{3}}{2}\)
=>\(7-AB^2=4\sqrt{3}\cdot\dfrac{\sqrt{3}}{2}=2\cdot3=6\)
=>AB=1
b: Xét ΔABC có \(AB^2+BC^2=CA^2\)
nên ΔABC vuông tại B
=>\(S_{BAC}=\dfrac{1}{2}\cdot BA\cdot BC=\dfrac{1}{2}\cdot1\cdot\sqrt{3}=\dfrac{\sqrt{3}}{2}\)
Độ dài đường trung tuyến kẻ từ A là:
\(m_A=\sqrt{\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}}=\sqrt{\dfrac{4+1}{2}-\dfrac{3}{4}}=\dfrac{\sqrt{7}}{2}\)

A B C M N
xét \(\Delta_{AMN}\)và \(\Delta_{ABN}\)
chung chiều cao hạ từ đỉnh N
AM=1/2AB
=>\(S\Delta_{ABN}=2.S\Delta_{AMN}=15.2=30cm^2\)
xét \(\Delta_{ABC}\)và \(\Delta_{ABN}\)
chung chiều cao hạ từ đỉnh B
AN=1/2AC
\(\Rightarrow S\Delta_{ABC}=2.S\Delta_{ABN}=30.2=60cm^2\)
vậy \(S\Delta_{ABC}=60cm^2\)

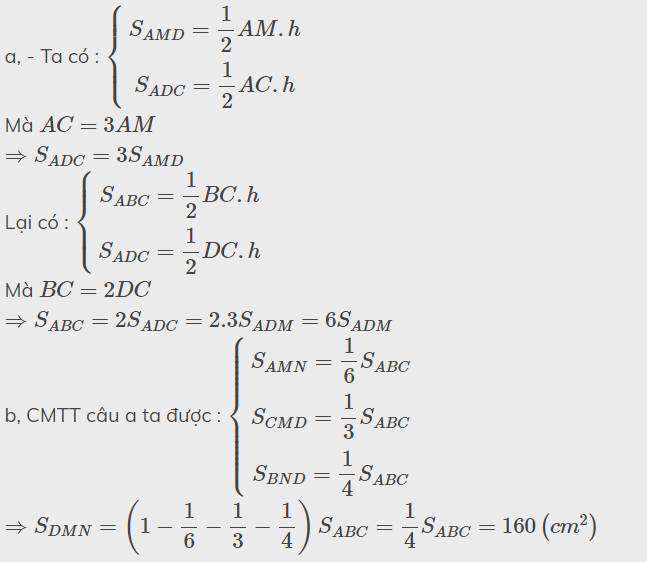
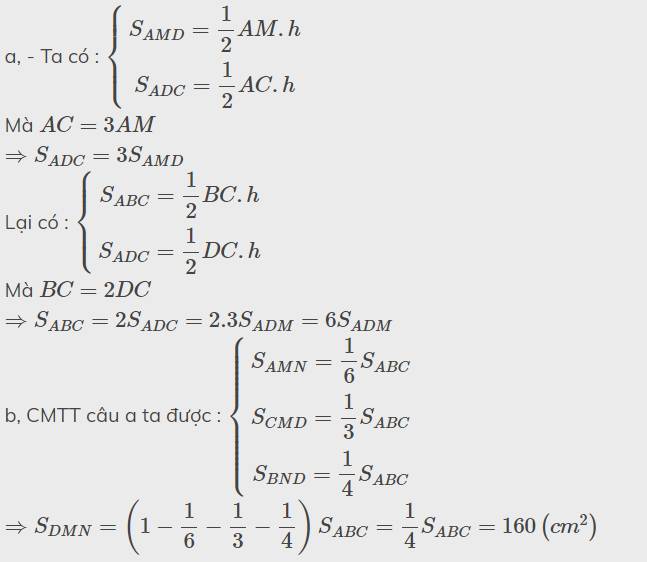
Tam giác đều nếu ta gọi độ dài 1 cạnh là thì độ dài đường cao sẽ là a3√/2
Đến đây thì dễ rùi tự làm nốt nhé!! Tick nha nguyen hai yen!!!