Cho tam giác ABC vuông tại A . Góc B=45 độ , AB=5cm .Tính BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
.jpg)
12 tháng 9 2016
Ta có: Tam giác ABC vuông và có góc B bằng 30 độ
=> góc C = 60 độ
=> Tam giác ABC là nửa tam giác đều
=> \(\frac{BC\sqrt{3}}{2}=AB=5\left(cm\right)\)
=> BC= \(\frac{5.2}{\sqrt{3}}=\frac{10}{\sqrt{3}}\)
=> AC = \(\frac{10}{\sqrt{3}}:2=\frac{5\sqrt{3}}{3}\) (cm)
=> AH = \(\frac{AB.AC}{BC}=\frac{5}{2}\left(cm\right)\)
b, Stam giác ABC=\(\frac{AB.AC}{2}=\frac{25\sqrt{3}}{6}\left(cm^2\right)\)
BA
17 tháng 3 2022
chịu................................................................................ ko hiểu
16 tháng 6 2017
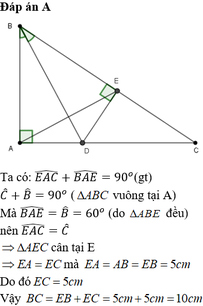
a) Tam giác ABD vuông và tam giác EBD vuông đều có cạnh BD
Suy ra góc ABD = góc EBD
Vậy tam giác ABD = tam giác EBD
b) Ta có: AB=EB ( tam giác ABD = tam giác EBD )
Suy ra tam giác ABE cân tại B
Tam giác ABE cân tại B có góc EBA =60 độ
Suy ra tam giác ABE là tam giác đều
c) Tam giác ABC có góc CAB = 90 độ, góc CBA = 60 độ
Suy ra ACB = 30 độ
Suy ra tam giác ABC là nửa tam giác đều
Suy ra AB = 1/2 BC
Suy ra BC = 2AB = 2 . 5 = 10 cm
8 tháng 3 2018
Vẽ xấu nhưng xem tạm thôi nhé!
a)Xét \(\Delta\)ABD (\(\widehat{A}=90^0\) )và \(\Delta\)EBD (\(\widehat{E}=90^0\))
Ta có:BD là cạnh chung (1)
\(\widehat{ABD}=\widehat{EBD}\) (gt) (2)
Từ (1) và (2) ==>\(\Delta ABD=\Delta EBD\) (CH+GN)
b)..............hình như tôi ko bt nx ^^
18 tháng 4 2018
Hình bn Hoa vẽ rồi !! mk k vẽ lại nữa
a ) Phương Hoa lm rồi
b) Vì tam giác ABD = tam giác EBD ( câu a )
=> AB = EB ( cặp cạnh tượng ứng )
=> tam giác ABE cân (1)
Mà góc ABE = 60 độ (2)
Từ (1) và (2) => tam giác ABE đều ( điều phải chứng minh )
c) Xét tam giác ABK và tam giác EBK có :
BD : cạnh chung
AB = BE ( vì tam giác ABE đều )
góc ABK = góc EBK = 30 độ ( vì BK là phân giác )
=> tam giác ABK = tam giác EBK ( c-g-c )
=> AK = EK ( cặp cạnh tương ứng )
Mà tam giác ABE đều => AB = EB = AE
=> AB = EB = AE = 5cm
mà AK + EK = AE
=> AK = AE = 2,5 cm
Mà AK = EC
=> AK = EC = 2,5cm
Vì BE + CE = BC
=> 5 + 2,5 = BC
=> BC = 7,5 cm
Chúc bn học tốt !!!
Ta có : \(\widehat{B}+\widehat{C}=90^o\) ( \(\Delta ABC\)vuông tại A )
\(45^o+\widehat{C}=90^o\)
\(\widehat{C}=90^o-45^o\)
\(\widehat{C}=45^o\)
Ta có : \(\widehat{B}=\widehat{C}=45^o\)
và \(\Delta ABC\)vuông tại A
\(\Rightarrow\Delta ABC\)vuông cân tại A
\(\Rightarrow AB=AC=5cm\)
Xét \(\Delta ABC\)vuông cân tai A ta có :
\(BC^2=AB^2+AC^2\)( ĐL Py - ta - go )
\(BC^2=5^2+5^2\)
\(BC^2=25+25\)
\(BC^2=50\)
\(\Rightarrow BC=\sqrt{50}\)
\(\Delta ABC\)vuông tại A có \(\widehat{B}=45^o\)
\(\Rightarrow\Delta ABC\)vuông cân tại A \(\Rightarrow AB=AC\)
Áp dụng định lý Pytago ta có: \(AB^2+AC^2=BC^2\)
\(\Rightarrow2AB^2=BC^2\)\(\Rightarrow BC^2=2.5^2=50\)
\(\Rightarrow BC=\sqrt{50}=\sqrt{25.2}=5\sqrt{2}\)
Vậy \(BC=5\sqrt{2}cm\)