Bài 1: cho các tập hợp
A là tập hợp các số tự nhiên mà 6 × X = 0
B { x N*, X + 6 = 6 }
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 9 2023
a) \(7+x=15\Rightarrow x=8\)
\(\Rightarrow A=\left\{8\right\}\)
b) \(x+2< 6\Rightarrow x< 4\)
\(\Rightarrow B=\left\{x\inℕ|x< 4\right\}\)
c) \(x+0=x\Rightarrow0x=0\Rightarrow\forall x\inℕ\)
\(\Rightarrow C=\left\{\forall x\inℕ\right\}\)
d) \(23-x< 6\Rightarrow x>17\)
\(\Rightarrow D=\left\{x\inℕ|x>17\right\}\)
CM
28 tháng 11 2019
a, x – 9 = 13 => x = 13 + 9 => x = 22
Vậy M = {22} và M có 1 phần tử
b, x + 6 = 34
x = 34 – 6
x = 28
Vậy H = {28} và H có 1 phần tử.
c, x.0 = 0 luôn đúng với mọi x ∈ N
Vậy O = N và O có vô số phần tử
d, a) x.0 = 3 không thỏa mãn vì trong tập hợp các số tự nhiên, số nào nhân với 0 cũng bằng 0
Vậy A = { ∅ } và A có 0 phần tử
e, (x – 2)(x – 5) = 0
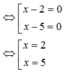
Vậy N = {2;5} và N có 2 phần tử
f, a) x : 0 = 0 không có số tự nhiên nào thỏa mãn vì không thể chia cho 0
Vậy G = { ∅ } và G có 0 phần tử
CM
7 tháng 4 2019
a. A = {8}. Vậy tập hợp A có 1 phần tử.
b. B = {0;1;2;…}. Vậy tập hợp B có vô số phần tử.
c. C = {5}. Vậy tập hợp C có 1 phần tử.
d. D = ∅ . Vậy tập hợp D không có phần tử nào.
e. E = {0;1;2;…}. Vậy tập hợp E có vô số phần tử.
f. F = ∅ . Vậy tập hợp F không có phần tử nào.
g. G = {0;1;2;3}. Vậy tập hợp G có 4 phần tử
22 tháng 8 2015
1) a) A = {18} có 1 phần tử
b) B = {0} có 1 phần tử
c) C = N có vô số phần tử
d) D = \(\phi\) không có phần tử nào
e) E = \(\phi\) không có phần tử nào
2) A = {0;1;2;...;9} , N = {0;1;2;;3;....9; 10; 11;....} => A \(\subset\) N
B = {0;2;4;6;8;10;12;...;...} => B \(\subset\) N
N * = {1;2;3;...} => N* \(\subset\) N
3) A = {4;5;6;...; 1999}
Từ 4 đến 1999 có 1999 - 4 + 1 = 1996 số => A có 1996 phần tử
B = {4; 6; 8 ...; 1998}
Từ 4 đến 1999 có 1996 số nên có 1996 : 2 = 998 số chẵn => B có 998 phần tử
C = {5;7;....; 1999} cũng có 998 phần tử
23 tháng 3 2016
zaugjhfhgadghjgfdbsfshdfdxgdxkfgughhgvhghzfxdjkhygdhzkhlzfhndkfhufhjfkdlkgnzjifhLhsdjkhtlhj.ldg,lhfgkhfg
A = {0}
B = {ø}
Biểu diễn :
+ Tập hợp A gồm các số tự nhiên mà \(6\times x=0\)
\(\Rightarrow A=\left\{0\right\}\)
b) Tập hợp \(B=\left\{x\inℕ^∗|x+6=6\right\}\)
Nên \(B=\left\{0\right\}\)