Cho P=2a/a-1 Tìm a thuộc Z để P nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A=2a2-a+2 = 2a2+a - 2a-1+3=a(2a+1)-(2a+1)+3=(2a+1)(a-1)+3
Để A chia hết cho (2a+1) thì 3 phải chia hết cho 2a+1. Vậy:
+/ 2a+1=1 => a=0
+/ 2a+1=3 => a=1


để x nguyên thì 2a - 1 phải là ước của 3
ta có:
2a - 1 = 1 => 2a = 1 + 1 = 2 => a = 2 : 2 = 1
2a - 1 = -1 => 2a = -1 + 1 = 0 => a = 0 : 2 = 0
2a - 1 = 3 => 2a = 3 + 1 = 4 => a = 4 : 2 = 2
2a - 1 = -3 => 2a = -3 + 1 = -2 => a = -2 : 2 = -1
vậy a \(\in\) {-1; 0; 1; 2}
Đễ X là số nguyên
=>\(\Rightarrow\frac{3}{2a-1}\in Z\Rightarrow2a-1\inƯ\left(3\right)=\left\{-1;1;3;-3\right\}\)
=>x={0;1;2;-1}

a) ĐKXĐ: \(x\ge0,x\ne9\)
\(A=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3}{\sqrt{x}+3}\)
b) \(A=\dfrac{3}{\sqrt{x}+3}=\dfrac{3}{\sqrt{64}+3}=\dfrac{3}{8+3}=\dfrac{3}{11}\)
c) \(2A=\dfrac{6}{\sqrt{x}+3}=1\Rightarrow\sqrt{x}+3=6\Rightarrow x=9\left(tm\right)\)
g) \(A=\dfrac{3}{\sqrt{x}+3}\in Z\)
\(\Rightarrow\sqrt{x}+3\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
Kết hợp đk:
\(\Rightarrow x\in\left\{0\right\}\)
h) \(A=\dfrac{3}{\sqrt{x}+3}\in Z\)
\(\Rightarrow\sqrt{x}+3\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
Kết hợp đk:
\(\Rightarrow x\in\left\{0\right\}\)
k) \(2A=\dfrac{6}{\sqrt{x}+3}=m\)

Vào đây:
Câu hỏi của LE NGUYEN HUYEN MI - Toán lớp 6 - Học toán với ...
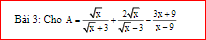
ĐKXĐ: a \(\ne\)1
Ta có: P = \(\frac{2a}{a-1}=\frac{2\left(a-1\right)+2}{a-1}=2+\frac{2}{a-1}\)
Để P nguyên <=> \(\frac{2}{a-1}\) nguyên
<=> 2 \(⋮\)a - 1
<=> a - 1 \(\in\)Ư(2) = {1; -1; 2; -2}
Lập bảng:
Vậy ....
\(P=\frac{2a}{a-1}\left(đkxđ:a\ne1\right)\)
\(P=\frac{2a}{a-1}=\frac{2\left(a-1\right)+2}{a-1}=2+\frac{2}{a-1}\)
Để P nguyên => \(\frac{2}{a-1}\)nguyên
=> \(2⋮a-1\) <=> \(a-1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
Cả 4 giá trị đều thỏa mãn ĐKXĐ
Vậy a thuộc các giá trị trên