Cho đường tròn tâm O đường kính AB cung C B có số đo bằng 45 độ M là một điểm nằm trên cung nhỏ AC Gọi N P là các điểm đối xứng với M theo thứ tự qua đường thẳng AB 0C số đo cung nhỏ NP là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 8 2020
Kéo dài CO cắt đường tròn tại Q \(\Rightarrow CQ\) là đường kính
Do \(\widehat{COB}=\widehat{AOQ}\) (đối đỉnh) \(\Rightarrow sđ\stackrel\frown{AQ}=sđ\stackrel\frown{BC}=45^0\) (từ sau bỏ chữ sđ cho lẹ, bạn tự hiểu)
Do P đối xứng M qua CQ nên \(\stackrel\frown{MQ}=\stackrel\frown{PQ}\)
Do N đối xứng M qua AB nên \(\stackrel\frown{AM}=\stackrel\frown{AN}\)
\(\stackrel\frown{NP}=\stackrel\frown{PQ}+\stackrel\frown{QN}=\stackrel\frown{MQ}+\stackrel\frown{QN}=\left(\stackrel\frown{MA}+\stackrel\frown{AN}+\stackrel\frown{QN}\right)\) \(+\stackrel\frown{QN}\)
\(=2\stackrel\frown{AN}+2\stackrel\frown{QN}=2\left(\stackrel\frown{AN}+\stackrel\frown{QN}\right)=2\stackrel\frown{AQ}=2.45^0=90^0\)
CH
Cô Hoàng Huyền
Admin
VIP
21 tháng 11 2017
a) Do AMNP là hình vuông nên \(\widehat{QMB}=45^o\)
Lại có do C là điểm chính giữa của nửa đường tròn nên \(\widebat{CB}=90^o\Rightarrow\widehat{CMB}=45^o\)
(Góc nội tiếp)
Vậy thì \(\widehat{CMQ}=\widehat{CMB}+\widehat{BMQ}=45^o+45^o=90^o\)
Vậy CQ là đường kính hay C và Q đối xứng nhau qua O.
b) Ta thấyAMNP là hình vuông. MI là phân giác góc \(\widehat{AMB}\) nên \(\Delta MAI=\Delta MNI\left(c-g-c\right)\Rightarrow\widehat{MAI}=\widehat{MNI}\)
Lại có \(\widehat{MAI}=\widehat{IAM}\) nên \(\widehat{MNI}=\widehat{IAM}\)
Xét tứ giác AINB có \(\widehat{MNI}=\widehat{IAM}\) nên AINB là tứ giác nội tiếp (góc ngoài tại đỉnh bằng góc đối diện)
13 tháng 7 2023
a: góc AID=1/2(sđ cung AD+sđ cung CB)
=1/2(sđ cung MD+sđ cung MC)
=1/2*sđ cung CD
=góc DAI
=>ΔAID cân tại D
b: góc PAI=góc PDI(1/2sđ cung MC=1/2sđ cung CB)
=>PDAI nội tiếp
16 tháng 2 2023
góc COB=40+110=150 độ
=>sđ cung nhỏ BC=150 độ
sđ cung lớn BC=360-150=210 độ
25 tháng 4 2023
a: góc EAB=1/2*90=45 độ
=>góc AEB=45 độ
b: góc EFD=góc FAB+góc FBA=90 độ+góc DAB
góc ECD+góc ACD=180 độ
=>góc ECD=góc DBA
=>góc EFD+góc ECD=180 độ
=>CDFE nội tiếp
CM
20 tháng 10 2019
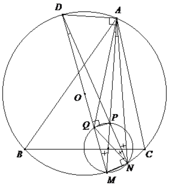
1). Vì MP là đường kính suy ra P N ⊥ M N (1).
Vì MD là đường kính suy ra D N ⊥ M N (2).
Từ (1) và (2), suy ra N; P; D thẳng hàng.
VT
24 tháng 2 2021
1. Gọi giao điểm của CH với AB là I, AH với BC là K,Ta có tứ giác BIHK nội tiếp mà (1) Ta lại có (hai góc nội tiếp cùng chắn một cung)
(t/c đối xứng) (2)Từ (1) và (2) Suy ra tứ giác AHCP nội tiếp.2. Tứ giác AHCP nội tiếp Ta lại có mà
(3)Chứng minh tương tự câu 1) ta có tứ giác AHBN nội tiếp
(4)
Từ (3) và (4) N, H, P thẳng hàng
3.
=> (<180độ) không đổi
Có AN = AM = AP, cần chứng minh NP = 2.AP.sinBAC
=> NP lớn nhất <=> AP lớn nhất mà AP = AM
AM lớn nhất <=> AM là đường kính của đường tròn (O)
Vậy NP lớn nhất <=> AM là đường kính của đường tròn.
24 tháng 2 2021
a)gọi I là giao điểm của CH và AB
K là giao điểm AH và BC
ta có :góc IBK+ AHC=180 độ
mà góc IBK= APC
=> tứ giác AHCP nội tiếp
b)Ta có Góc AHP= ACP cùng chắn cung AP (
mà góc ACP=ACM (1)
=> góc ACP= AHP
cmtt
gócAHN=ABN cùng chắn cung AP
mà ABN=ABM => AHN=ABM(2)
Xét tứ giác ABMC nội tiếp
gócACM+ABM=180 độ (3)
từ (1)(2)(3) =>
góc AHP+AHN=180 độ
=> N,H,P thẳng hàng
ta có góc MAN=2BAM,
góc MAP=2MAC
=> NAP=2(BAM+MAC)
=2 x góc BAC (ko đổi )
ta có AM=AN=AP
NP=2AP.sin BAC=2AM.sinBAC
=> NP lớn nhất <=> AM Max