cho 7 bạn nữ và 7 bạn nam ngồi quanh 1 bàn tròn. chứng minh rằng tồn tại 1 bạn ngồi giữa hai bạn nữ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 2 2020
Bạn tham khảo đề bài và cách làm của bài này rồi làm tương tự bài mà bạn đang cần giải đáp nha !!/ :
Có 15 nam và 15 nữ ngồi xung quanh một bàn tròn. Chứng minh rằng tồn tại 6 người ngồi cạnh nhau trong đó có đúng 3 nam và 3 nữ,
Bài làm
Giả sử không chọn được nhóm 6 bạn thỏa mãn yêu cầu bài toán.
Ta đánh số thứ tự cho các bạn nam từ 11 đến 1515 theo chiều kim đồng hồ, gọi xixi là số bạn nữ giữa bạn nam thứ ii và i+1(1≤i≤14)i+1(1≤i≤14) và x15x15 là số bạn nữ giữa bạn nam thứ 1515 và thứ 11.
Ta có 15∑1xi=15∑115xi=15
Điều kiện để chọn ra nhóm 6 bạn ngồi cạnh nhau mà thỏa mãn điều kiện bài toán là tồn tại ii sao cho xi+xi+1≤3xi+xi+1≤3 và trong hai số xi−1,xi+2xi−1,xi+2 luôn có một số mà tổng nó với xi,xi+1xi,xi+1 không nhỏ hơn 3.
Nếu trong xixi tồn tại một số không nhỏ hơn 3, giả sử x1≥3x1≥3, nếu x2+x3≤3x2+x3≤3 thì ta chọn được bạn nam số 2,3,42,3,4 (vô lý); do đó x2+x3≥4x2+x3≥4, nếu x3+x4≥3x3+x4≥3 thì ta chọn được bạn nam số 3,4,53,4,5 (vô lý), do đó x3+x4≥4x3+x4≥4, cứ làm như vậy ta được xi+xi+1≥4(2≤i≤14)xi+xi+1≥4(2≤i≤14), suy ra 15∑1xi=x1+(x2+x3)+...+(x14+x15)≥3+7.4>15∑115xi=x1+(x2+x3)+...+(x14+x15)≥3+7.4>15 (vô lý).
Do đó xixi chỉ nhận các giá trị 0,1,20,1,2, nếu xi=1xi=1 với mọi ii thì ta điều giả sử vô lý do đó trong xixi có ít nhất 1 số bằng 00 và 1 số bằng 22.
Ta viết dãy xixi thành dãy 15 số 0,1,20,1,2, nhận thấy số số 0 phải bằng số số 2.
Vì có ít nhất một số 2 nên không mất tính tổng quát giả sử số đầu tiên là 2, nếu có tồn tại hai số 1 và 2 hoặc hai số 2 nằm liên tiếp nhau thì ta có thể chọn được các bạn thỏa mãn bài toán (vô lý với giả sử) nên ta với mỗi số 2 thì hai bên cạnh nó phải là hai số 0. Do đó số số 0 nhiều hơn số số 2(vô lý)(số số 0 bằng số số 2 chỉ trong trường hợp dãy có chẵn số và các số 2, 0 xếp xen kẽ nhau nhưng dãy có 15 số nên điều này không xảy ra được).
Vậy điều giả sử sai, luôn chọn được nhóm 6 bạn thỏa mãn yêu cầu bài toán.
18 tháng 5 2017
Số cách xếp quanh bàn tròn là \(n\left(\Omega\right)=9!\)
Kí hiệu A là biến cố : "Nam nữ ngồi xen kẽ nhau"
Ta có :
\(n\left(A\right)=4!5!\) và \(P\left(A\right)=\dfrac{4!5!}{9!}\approx0,008\)
CM
15 tháng 7 2019
a) Xếp 6 nam vào 6 ghế cạnh nhau. Có 6! cách.
Giữa các bạn nam có 5 khoảng trống cùng hai đầu dãy, nên có 7 chỗ có thể đặt ghế cho nữ.
Bây giờ chọn 4 trong 7 vị trí để đặt ghế. Có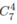 
cách.
Xếp nữ vào 4 ghế đó. Có 4! cách.
Vậy có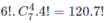 
cách xếp mà không có hai bạn nữ nào ngồi cạnh nhau.
b) Xếp 6 ghế quanh bàn tròn rồi xếp nam vào ngồi. Có 5! cách.
Giữa hai nam có khoảng trống. Xếp 4 nữ vào 4 trong 6 khoảng trống đó. Có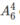 
cách.
Theo quy tắc nhân, có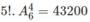 
cách.
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 7 2021
Coi 2 bạn nữ và cô giáo là 1 nhóm, kết hợp với 3 bạn nam ta được 4 "người"
Hoán vị 4 người trên bàn tròn: \(3!=6\) cách
Xếp cô giáo và 2 bạn nữ: \(2!=2\) cách
Tổng cộng: \(6.2=12\) cách