Hai tam giác ABC và A'B'C' có độ dài lần lượt là:
a,3cm, 4cm, 5cm và 9cm, 12cm, 15cm
b, 7cm, 8cm, 9cm và 8cm, 9cm, 12cm
Hãy xếp sự đồng dạng của 2 tam giác trong 2 trường hợp trên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hai tam giác ABC và tam giác MNP có A ^ = M ^ , B ^ = N ^ .
Để hai tam giác ABC và MNP bằng nhau cần điều kiện A B = M N theo trường hợp góc – cạnh – góc .
Chọn đáp án B.

Xét ΔABC vuông tại A và ΔDEF vuông tại D có
BC=EF(gt)
AC=DF(gt)
Do đó: ΔABC=ΔDEF(cạnh huyền-cạnh góc vuông)
Cách 1:
Xét tam giác $ABC$ và $DEF$ có:
$\widehat{A}=\widehat{D}=90^0$
$BC=EF$
$AC=DF$
$\Rightarrow \triangle ABC=\triangle DEF$ (ch-gcv)
Cách 2:
Vì $BC=EF; AC=DF\Rightarrow BC^2-AC^2=EF^2-DF^2$ hay $BA^2=ED^2$
$\Leftrightarrow BA=ED$ (theo định lý Pitago)
Hai tam giác $ABC$ và $DEF$ có các cạnh $AB=DE, BC=EF, AC=DF$ nên bằng nhau theo TH c.c.c

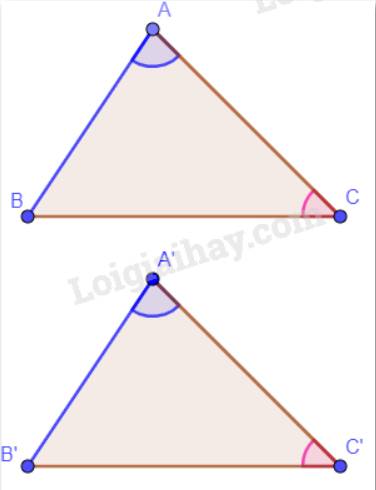
Vì \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\)mà tổng ba góc trong một tam giác bằng 180° nên \(\widehat B = \widehat {B'}\).
Xét hai tam giác ABC và A’B’C’ có: \(\widehat A = \widehat {A'}\), AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
Lời giải:
a) Ta thấy: $\frac{3}{9}=\frac{4}{12}=\frac{5}{15}$
$\Leftrightarrow \frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{CA}{C'A'}$
$\Rightarrow \triangle ABC\sim \triangle A'B'C'$ (c.c.c)
b)
\(\frac{8}{8}=\frac{9}{9}\Leftrightarrow \frac{BC}{A'B'}=\frac{CA}{B'C'}=1\). Tỷ số này khác với $\frac{AB}{C'A'}(=\frac{7}{12})$
Nên không tồn tại 2 tam giác đồng dạng trong TH này.