Cho tam giác ABC có AB:5x+y-5=0,AC:7x-y-19=0
B(1;0),C(3;2)
a) Viết pt cạnh BC ,đường cao BH, tiếp tuyến CC'
b)Viết pt đtròn (C) tâm A đi qua C
c) Viết pt đt ròn (C) đường kính BC
d) Viết pt đtròn (C) ngoại tiếp tam giác ABC
CẦN GẤP LẮM Ạ !!!! Help em vs .Cảm ơn ạ!


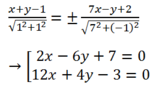
\(\overrightarrow{BC}=\left(2;2\right)=2\left(1;1\right)\)
\(\Rightarrow\) đường thẳng BC nhận \(\left(1;-1\right)\) là 1 vtpt
Phương trình BC: \(1\left(x-1\right)-1\left(y-0\right)=0\Leftrightarrow x-y-1=0\)
BH vuông góc AC nên nhận \(\left(1;7\right)\) là 1 vtpt
Pt BH qua B: \(1\left(x-1\right)+7\left(y-0\right)=0\Leftrightarrow x+7y-1=0\)
Chắc bạn ghi sai đề, làm gì có tiếp tuyến CC'?
b/ A là giao điểm AB và AC nên tọa độ thỏa: \(\left\{{}\begin{matrix}5x+y-5=0\\7x-y-19=0\end{matrix}\right.\) \(\Rightarrow A\left(2;-5\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(1;7\right)\Rightarrow R=AC=\sqrt{1^2+7^2}=\sqrt{50}\)
Pt đường tròn: \(\left(x-2\right)^2+\left(y+5\right)^2=50\)
c/ \(\overrightarrow{BC}=\left(2;2\right)\Rightarrow BC=\sqrt{2^2+2^2}=2\sqrt{2}\)
Gọi M là trung điểm BC \(\Rightarrow M\left(2;1\right)\) \(\Rightarrow\) M là tâm đường tròn
\(R=BM=\frac{BC}{2}=\sqrt{2}\)
Phương trình: \(\left(x-2\right)^2+\left(y-1\right)^2=2\)
d/ Trung trực d của BC qua M và vuông góc BC có pt:
\(1\left(x-2\right)+1\left(y-1\right)=0\Leftrightarrow x+y-3=0\)
Gọi N là trung điểm AC \(\Rightarrow N\left(\frac{5}{2};-\frac{3}{2}\right)\)
Trung trực d' của AC qua N và vuông góc AC có pt:
\(1\left(x-\frac{5}{2}\right)+7\left(y+\frac{3}{2}\right)=0\Leftrightarrow x+7y+8=0\)
Gọi I là tâm đường tròn ngoại tiếp tam giác => I là giao của d và d'
Tọa độ I thỏa mãn: \(\left\{{}\begin{matrix}x+y-3=0\\x+7y+8=0\end{matrix}\right.\) \(\Rightarrow I\left(\frac{29}{6};-\frac{11}{6}\right)\)
\(\Rightarrow\overrightarrow{IB}=\left(-\frac{23}{6};\frac{11}{6}\right)\Rightarrow R=IB=\frac{5\sqrt{26}}{6}\)
Pt: \(\left(x-\frac{29}{6}\right)^2+\left(y+\frac{11}{6}\right)^2=\frac{325}{18}\)
Bạn kiểm tra lại tính toán