Trong hệ mặt phẳng tọa độ Oxy, viết pt đg thg d biết d vuông góc với ∆: 2x-y+1=0 và cắt đg tròn (C): \(x^2+y^2+2x-4y-4=0\) theo một dây cung có độ dài bằng 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
31 tháng 5 2021
1.
\(\left(C\right):x^2+y^2-2x-4=0\)
\(\Leftrightarrow\left(x-1\right)^2+y^2=5\)
Đường tròn \(\left(C\right)\) có tâm \(I=\left(1;0\right)\), bán kính \(R=\sqrt{5}\)
Phương trình đường thẳng \(d_1\) có dạng: \(x+y+m=0\left(m\in R\right)\)
Mà \(d_1\) tiếp xúc với \(\left(C\right)\Rightarrow d\left(I;d_1\right)=\dfrac{\left|1+m\right|}{\sqrt{2}}=\sqrt{5}\)
\(\Leftrightarrow\left|m+1\right|=\sqrt{10}\)
\(\Leftrightarrow m=-1\pm\sqrt{10}\)
\(\Rightarrow\left[{}\begin{matrix}d_1:x+y-1+\sqrt{10}=0\\d_1:x+y-1-\sqrt{10}=0\end{matrix}\right.\)
HP
31 tháng 5 2021
2.
Phương trình đường thẳng \(\Delta\) có dạng: \(x-y+m=0\left(m\in R\right)\)
Ta có: \(d\left(I;\Delta\right)=\sqrt{R^2-\dfrac{MN^2}{4}}=2\)
\(\Leftrightarrow\dfrac{\left|m+1\right|}{\sqrt{2}}=2\)
\(\Leftrightarrow m=-1\pm2\sqrt{2}\)
\(\Rightarrow\left[{}\begin{matrix}\Delta:x-y+1+2\sqrt{2}=0\\\Delta:x-y+1-2\sqrt{2}=0\end{matrix}\right.\)
CM
6 tháng 11 2017
Đáp án C
- Đường thẳng d’ song song với d nên có dạng: 3x+ y+ m= 0
- IH là khoảng cách từ I đến d’:
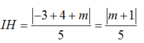
- Xét tam giác vuông IHB:
28 tháng 2 2023
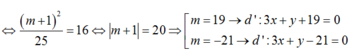
(3):
a: =>căn 2x-3=x-3
=>x>=3 và x^2-6x+9=2x-3
=>x>=3 và x^2-8x+12=0
=>x=6
b: =>x>=-1 và 2x^2+mx-3=x^2+2x+1
=>x>=-1 và x^2+(m-2)x-4=0
=>với mọi m thì pt luôn có hai nghiệm phân biệt lớn hơn -1 vì a*c<0
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 5 2019
Đường tròn (C) tâm \(I\left(-1;4\right)\) bán kính \(R=5\)
Do d' song song d nên pt d' có dạng: \(3x+y+c=0\)
Áp dụng định lý Pitago ta có:
\(d\left(I;d'\right)=\sqrt{R^2-3^2}=4\)
\(\Rightarrow\frac{\left|-1.3+4+c\right|}{\sqrt{3^2+1^2}}=4\Leftrightarrow\left|c+1\right|=4\sqrt{10}\Rightarrow\left[{}\begin{matrix}c=4\sqrt{10}-1\\c=-4\sqrt{10}-1\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}3x+y+4\sqrt{10}-1=0\\3x+y-4\sqrt{10}-1=0\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2020
Bài 38:
Thay phương trình d2 vào d1 ta được:
\(2\left(-1+3t\right)+\left(2+t\right)-7=0\)
\(\Leftrightarrow7t-7=0\Rightarrow t=1\)
\(\Rightarrow\left\{{}\begin{matrix}m=-1+3t=2\\n=2+t=3\end{matrix}\right.\)
\(\Rightarrow P=7\)
Bài 39:
Gọi tọa độ A(a;0) và tọa độ B(0;b)
Do M là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}\frac{a+0}{2}=3\\\frac{b+0}{2}=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=6\\b=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A\left(6;0\right)\\B\left(0;2\right)\end{matrix}\right.\)
Phương trình AB: \(\frac{x}{6}+\frac{y}{2}=1\Leftrightarrow x+3y-6=0\)
Bài 40:
d có 1 vtcp là \(\left(3;-4\right)\)
Gọi d' là đường thẳng qua M và vuông góc d \(\Rightarrow\) d' có 1 vtpt là \(\left(3;-4\right)\)
Phương trình d':
\(3\left(x-2\right)-4\left(y+5\right)=0\Leftrightarrow3x-4y-26=0\)
N là giao của d và d' nên tọa độ N thỏa mãn:
\(3\left(-7+3t\right)-4\left(2-4t\right)-26=0\Rightarrow t=\frac{11}{5}\)
\(\Rightarrow\left\{{}\begin{matrix}x_N=-7+3t=-\frac{2}{5}\\y_N=2-4t=-\frac{34}{5}\end{matrix}\right.\) \(\Rightarrow N\left(-\frac{2}{5};-\frac{34}{5}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2020
Bài 35:
Do \(AB//CD\) nên đường thẳng AB nhận \(\left(2;5\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x-4\right)+5\left(y+1\right)=0\Leftrightarrow2x+5y-3=0\)
Bài 36:
Do đường thẳng song song trục hoành nên có dạng \(y=a\)
Do đường thẳng qua A(1;3) nên pt là \(y=3\)
Bài 37:
Do thẳng thẳng vuông góc trục hoành nên có dạng \(x=a\)
Đường thẳng qua A(1;3) nên có pt: \(x=1\)
Đường tròn (C) tâm \(I\left(-1;2\right)\) bán kính \(R=\sqrt{\left(-1\right)^2+2^2+4}=3\)
Áp dụng định lý Pitago:
\(d\left(I;d\right)=\sqrt{R^2-\left(\frac{6}{2}\right)^2}=0\)
\(\Rightarrow d\) đi qua I
d vuông góc \(\Delta\) nên d nhận \(\left(1;2\right)\) là 1 vtpt
Phương trình d:
\(1\left(x+1\right)+2\left(y-2\right)=0\Leftrightarrow x+2y-3=0\)