rs=100m
mq=...m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Có: \(Ry\perp RS\Rightarrow\widehat{SRy}=90^o\\ Rx\perp RT\Rightarrow\widehat{TRx}=90^o\)
Có: \(\widehat{SRx}=\widehat{SRT}+\widehat{TRx}\\ \widehat{TRy}=\widehat{SRT}+\widehat{SRy}\)
Mà \(\widehat{TRx}=\widehat{SRy}\left(=90^o\right)\)
\(\Rightarrow\widehat{SRx}=\widehat{TRy}\)
b) Xét ΔSRM và ΔTRN có:
\(RS=RT\left(gt\right)\\ \widehat{SRx}=\widehat{TRy}\left(cmt\right)\\ RM=RN\left(gt\right)\)
\(\Rightarrow\Delta SRM=\Delta TRN\left(c.g.c\right)\\ \Rightarrow SM=TN\left(\text{2 cạnh tương ứng}\right)\)

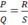 ⇒ PS = QR (1) và P ≠ Q, R ≠ S
⇒ PS = QR (1) và P ≠ Q, R ≠ S
Trừ từng vế đẳng thức (1) với PR: PS – PR = QR – PR
⇒ P(S – R) = R(Q – P) 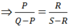

Xuất phát từ điều cần chứng minh Û P(S + R) = R(Q + P)
Rút gọn còn PS = RQ hay P Q = R S (đúng với giả thiết).

a. PTPU : R + S \(\underrightarrow{t^o}\) RS
b. nS =6,4 : 32 = 0,2 mol
Theo PTPU : nR = nS = 0,2 mol
→MR=4,8 : 0,2 = 24 →R là Magie(Mg)
PTPU : Mg + S → MgS
Theo PTPU ; nMgS = nS = 0,2 mol
→ mMgS = 0,2(24 + 32) = 11,2 g

Nếu 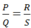 ⇒ PS = QR (1). Vì
⇒ PS = QR (1). Vì 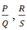 là phân thức
là phân thức
⇒ Q, S khác không. Cộng vào hai vế của đẳng thức (1) với QS
PS + QS = QR + QS ⇒ (P + Q).S = Q.(R + S)
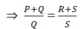

Xuất phát từ điều cần chứng minh
Rút gọn còn PS = RQ hay P Q = R S .

T V R S Z K
Trong sách nó vẽ dài dòng qua mình rút gọn lại .
Lời giải ...........................
Ta có :
\(TV\) // \(RS\)
\(TZ=ZR\) và \(VK=KS\)
\(\Rightarrow ZK=\dfrac{1}{2}\left(TV+RS\right)\)
\(\Rightarrow TV+RS=ZK:\dfrac{1}{2}\)
\(\Rightarrow TV+RS=2ZK\left(đpcm\right)\)
Kẻ ZY // TV (Y thuộc RV )
- Xét tam giác RTV CÓ :
ZY // TV
Z là trung điểm TR
Suy ra Y là trung điểm RV
Suy ra 2ZY = TV (*)
- Xét tam giác VRS có :
Y là trung điểm RV
K là trung điểm VS
Suy ra YK // RS
Suy ra 2YK = RS (**)
- Vì ZY // RS và YK // RS
Suy ra Z , Y , K thẳng hàng
Suy ra ZY + YK = ZK (***)
Từ (*) , (**) , (***)
Suy ra TV + RS = 2ZY + 2YK = 2(ZY +YK ) = 2ZK
Câu hỏi của em chưa được rõ ràng, không hiểu em cần hỏi điều gì với dữ liệu này?