Question

[Trần Quốc Tuấn hi]

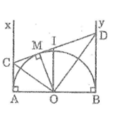
Cho đuờng tròn tâm O có duong kính AB. Trên cùng nua mặt phăng có bờ là duong thang AB, ve các tiép tuyén Ax, By của duong tròn tâm O và một diêm C thuộc (O) (C khác A, B). Tiếp tuyến tại C của đuờng tròn (O) cat Ax và By lần luợt tại D, E.

a) Chứng minh: DE = AD + BE và C, O, B, E cung thuộc một duong tròn.

b) OE cat (O) lần lugt tại V, K và cắt BC tại L (V nåm giữa O và E). Chúng minh: LO . LE = LV. LK.

c ) \(\frac{1}{VL}-\frac{1}{VE}=\frac{2}{KV}\)

Answer 1

[Nguyễn Hoàng Bảo Nhi]

Answer 2

[Nguyễn Hoàng Bảo Nhi]

a.Vì  DC,DA là tiếp tuyến của (O) \(\Rightarrow DC=DA\)

Tương tự \(EC=EB\Rightarrow DE=DC+CE=AD+BE\)

Mà EC,EB là tiếp tuyến của (O) \(\Rightarrow EC\perp OC,EB\perp OC\)

=> C,O,B,E cùng thuộc một đường tròn đường kính OE

b ) Ta có : EB,EC là tiếp tuyến của (O) \(\Rightarrow EO\perp CB=L\)

Mà VL là đường kính của (O)

\(\Rightarrow LK.LV=CL^2=LO.LE\)

c.Ta có :

\(\widehat{VCL}=\widehat{CBV}=\widehat{ECV}\) vì EC là tiếp tuyến của (O)

\(\Rightarrow CV\) là phân giác \(\widehat{ECL}\)

\(\Rightarrow\frac{VL}{VE}=\frac{CL}{CE}\)

Lại có : \(\Delta CLE~\Delta OCE\left(g.g\right)\)

\(\Rightarrow\frac{CL}{CE}=\frac{OC}{OE}\)

Lại có : \(OC^2=OL.OE\Rightarrow\frac{OC}{OE}=\frac{OL}{OC}\)

\(\Rightarrow\frac{VL}{VE}=\frac{OC}{OE}=\frac{OL}{OC}\)

\(\Rightarrow\frac{VL}{VE}=\frac{OL}{R}\)

\(\Rightarrow\frac{VL}{VE}+\frac{2VL}{KV}=\frac{OL}{R}+\frac{2VL}{KV}\)

\(\Rightarrow\frac{VL}{VE}+\frac{2VL}{KV}=\frac{OL}{R}+\frac{2VL}{2R}\)

\(\Rightarrow\frac{VL}{VE}+\frac{2VL}{KV}=\frac{OL}{R}+\frac{VL}{R}\)

\(\Rightarrow\frac{VL}{VE}+\frac{2VL}{KV}=\frac{OL+VL}{R}\)

\(\Rightarrow\frac{VL}{VE}+\frac{2VL}{KV}=\frac{R}{R}=1\)

\(\Rightarrow\frac{1}{VL}-\frac{1}{VE}=\frac{2}{KV}\)