Cho (O),dây AB = 30cm,bán kính (O) là 17cm.Gọi O là trung điểm của AB.Tính OI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AQ
1
24 tháng 10 2021
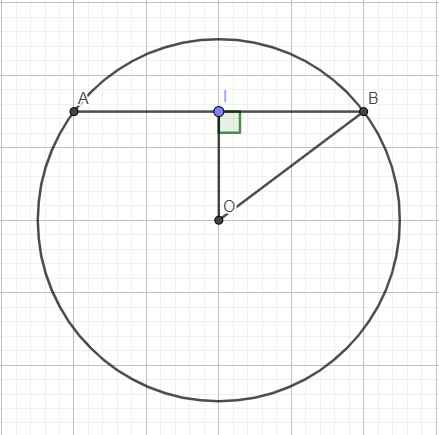
Vì I là trung điểm AB nên \(AI=\dfrac{1}{2}AB=15\left(cm\right)\)
Vì AB là dây cung nên \(OA=OB=R_{\left(O;OA\right)}=17\left(cm\right)\)
Vì I là trung điểm dây AB nên OI⊥AB
Áp dụng PTG: \(OI=\sqrt{OA^2-AI^2}=\sqrt{17^2-15^2}=8\left(cm\right)\)
ZT
1
24 tháng 10 2021
sửa đề I là trung điểm AB
Vì I là trung điểm AB => OI vuông AB
AI = IB = AB/2 = 15 cm ( I là trung điểm )
Theo định lí Pytago tam giác AIO vuông tại I
\(OI=\sqrt{AO^2-AI^2}=8\)cm
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 10 2021
Do I là trung điểm AB \(\Rightarrow OI\perp AB\)
Ta có: \(IB=\dfrac{1}{2}AB=4\left(cm\right)\)
Áp dụng định lý Pitago trong tam giác vuông OIB:
\(OI^2+IB^2=OB^2\)
\(\Rightarrow OI=\sqrt{OB^2-IB^2}=\sqrt{5^2-4^2}=3\left(cm\right)\)
25 tháng 8 2023
a: ΔOAB cân tại O
mà OI là đường trung tuyến
nên OI vuông góc AB
I là trung điểm của AB
=>IA=IB=16/2=8cm
ΔOIA vuông tại I
=>OA^2=OI^2+IA^2
=>OI^2=10^2-8^2=36
=>OI=6(cm)
b: OM=OI+IM
=>6+IM=10
=>IM=4cm
ΔMIA vuông tại I
=>MI^2+IA^2=MA^2
=>\(MA=\sqrt{4^2+8^2}=4\sqrt{5}\left(cm\right)\)
19 tháng 11 2023
a: ΔOAB cân tại O
mà OI là đường trung tuyến
nên OI là đường cao và OI là phân giác của \(\widehat{AOB}\)
Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
=>\(\widehat{OBC}=\widehat{OAC}=90^0\)
=>CB là tiếp tuyến của (O)
b: I là trung điểm của AB
=>IA=IB=AB/2=12cm
ΔOIA vuông tại I
=>\(OI^2+IA^2=OA^2\)
=>\(OI^2+12^2=13^2\)
=>\(OI^2=169-144=25\)
=>\(OI=\sqrt{25}=5\left(cm\right)\)
Xét ΔOAC vuông tại A có AI là đường cao
nên \(OI\cdot OC=OA^2\)
=>\(OC\cdot5=13^2=169\)
=>OC=33,8(cm)
Xét ΔOIA vuông tại I có
\(OA^2=OI^2+IA^2\)
hay OI=8(cm)