Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

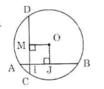
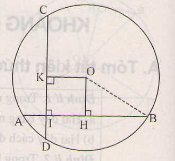
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra: J là trung điểm của AB.
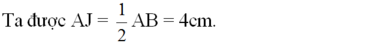
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 (OA = R = 5cm)
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.
b) Kẻ OM vuông góc với CD tại M.
Tứ giác OJIM có: 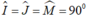 nên là hình chữ nhật
nên là hình chữ nhật
Ta có IJ = AJ – AI = 4 – 1 = 3cm
=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)
Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)

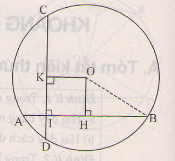
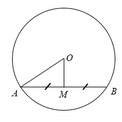
a) Vẽ OH⊥ABOH⊥AB, ta có HA=HB=4cm.
Xét tam giác HOB vuông tại H, có:
OH2=OB2−HB2=52−42=9⇒OH=3(cm)OH2=OB2−HB2=52−42=9⇒OH=3(cm).
b) Vẽ OK⊥CDOK⊥CD. TỨ giác KOHI có ba góc vuông nên là hình chữ nhật, suy ra OK=HI. Ta có HI=4-1=3cm, suy ra OK=3cm.
Vậy OH=OK=3cm.
Hai dây AB và CD cách đều tâm nên chúng bằng nhau.
Do đó AB=CD.
a) Vẽ OH ⊥ AB, ta có HA=HB=4cm.
Xét tam giác HOB vuông tại H, có:
OH2 = OB2 – HB2 =52 – 42 = 9
⇒ OH = 3(cm).
b) Vẽ OK ⊥ CD. Tứ giác KOHI có ba góc vuông nên là hình chữ nhật, suy ra OK=HI.
Ta có HI=4-1=3cm, suy ra OK=3cm.
Vậy OH=OK=3cm. Hai dây AB và CD cách đều tâm nên chúng bằng nhau.
Do đó AB=CD.

Đáp án A
Vì M là trung điểm của AB nên ta có: 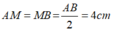
Theo quan hệ vuông góc giữa đường kính và dây ta có:
OM ⊥ AB
Áp dụng định lí Pytago vào tam giác OAM ta có:
O M 2 = O A 2 - A M 2 = 52 - 42 = 9 ⇒ O M = 3 c m

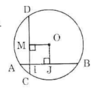
Kẻ OM vuông góc với CD tại M.
Tứ giác OJIM có: 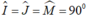 nên là hình chữ nhật
nên là hình chữ nhật
Ta có IJ = AJ – AI = 4 – 1 = 3cm
=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)
Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)

D M A J C O J B
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra : J là trung điểm của AB
Ta được : \(AJ=\frac{1}{2}AB=4cm\)
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 ( OA = R = 5cm )
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.
b) Kẻ OM vuông góc với CD tại M.
Tứ giác OJIM có :\(\widehat{I}=\widehat{J}=\widehat{M}=90^o\)nên là hcn
Ta có IJ = AJ – AI = 4 – 1 = 3cm
=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)
Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)
Do I là trung điểm AB \(\Rightarrow OI\perp AB\)
Ta có: \(IB=\dfrac{1}{2}AB=4\left(cm\right)\)
Áp dụng định lý Pitago trong tam giác vuông OIB:
\(OI^2+IB^2=OB^2\)
\(\Rightarrow OI=\sqrt{OB^2-IB^2}=\sqrt{5^2-4^2}=3\left(cm\right)\)