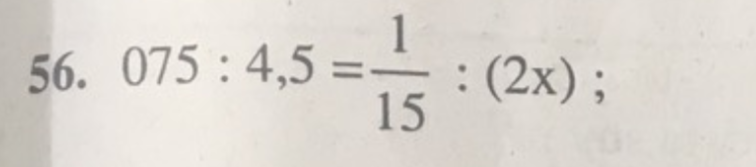ai làm giúp em với đang gấp lắm ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
0
ai làm giúp mình với mình đang cần gấp lắm ạ
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 1
\(\widehat{XAB}\) + \(\widehat{ABZ}\) = 1300 + 500 = 1800
Vì góc XAB và góc ABZ là hai góc trong cùng phía nên
Ax // BZ
BZ // Cy ⇔ \(x\) + \(\widehat{yCB}\) =1800
⇒ \(x\) = 1800 - 1450 = 350
D
1
2 tháng 7 2023
3:
a:Các tia trên hình là Ax,Ay,Bx,By,Cx,Cy
=>Có 6 tia
b: AB<AC
=>B nằm giữa A và C
=>AB+BC=AC
=>BC=4cm
c: AI=3/2=1,5cm
CI=7-1,5=5,5cm
ML
1
5 tháng 1 2022
Bài 3:
\(a,\) Gọi \(\left(d\right):y=ax+b\) là đt cần tìm
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\\0a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\Leftrightarrow\left(d\right):y=2x+1\)
\(b,\) PT hoành độ giao điểm:
\(-x^2=2x+1\Leftrightarrow\left(x+1\right)^2=0\Leftrightarrow x=-1\Leftrightarrow y=-1\Leftrightarrow A\left(-1;-1\right)\)
Vậy \(A\left(-1;-1\right)\) là tọa độ giao điểm (P) và (d)
Bài 4:
PT có 2 nghiệm \(\Leftrightarrow\Delta'=16-3m\ge0\Leftrightarrow m\le\dfrac{16}{3}\)
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{8}{3}\\x_1x_2=\dfrac{m}{3}\end{matrix}\right.\)
Mà \(x_1^2+x_2^2=\dfrac{82}{9}\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=\dfrac{82}{9}\)
\(\Leftrightarrow\dfrac{64}{9}-\dfrac{2m}{3}=\dfrac{82}{9}\\ \Leftrightarrow\dfrac{2m}{3}=-2\Leftrightarrow m=-3\left(tm\right)\)
P
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
0
BT
7
13 tháng 7 2021
1) Ta có: \(\sqrt{2x+5}=\sqrt{3-x}\)
\(\Leftrightarrow2x+5=3-x\)
\(\Leftrightarrow2x+x=3-5\)
\(\Leftrightarrow3x=-2\)
hay \(x=-\dfrac{2}{3}\)
2) Ta có: \(\sqrt{2x-5}=\sqrt{x-1}\)
\(\Leftrightarrow2x-5=x-1\)
\(\Leftrightarrow2x-x=-1+5\)
\(\Leftrightarrow x=4\)
PN
23 tháng 8 2021
3 , \(PT\left(đk:\frac{16}{3}\ge x\ge3\right)< =>x^2-3x=16-3x\)
\(< =>x^2-16=0< =>\left(x-4\right)\left(x+4\right)=0< =>\orbr{\begin{cases}x=4\left(tm\right)\\x=-4\left(ktm\right)\end{cases}}\)
4 , \(PT\left(đk:...\right)< =>2x^2-3=4x-3< =>2x^2-4x=0\)
\(< =>2x\left(x-2\right)=0< =>\orbr{\begin{cases}x=0\left(...\right)\\x=2\left(...\right)\end{cases}}\)
bạn tự tìm đk rồi đối chiếu nhé :P
\(\dfrac{\dfrac{1}{15}}{2x}=\dfrac{75}{4.5}\)
\(\Leftrightarrow2x=\dfrac{1}{250}\)
hay \(x=\dfrac{1}{500}\)