Cho \(\bigtriangleup\text{ABC}\)vuông tại A với đường cao AH (\(H\ne B\text{ và }C\)) và I là trung điểm của AB. Trên tia HI lấy điểm D sao cho ID = IH.
a) Định dạng \(\diamond\text{DAHB}\) ?
b) Trên AC lấy O là trung điểm. Chứng minh \(\diamond\text{IOCB}\) là hình gì ?
c) Cho biết \(IO\cap AH=\left\{O_2\right\}\). Từ O kẻ đường thẳng vuông góc với BC cắt BC ở H2. Chứng minh \(H_2O=HO_2\).
d) Chứng minh \(\Delta\text{AO}_2\text{O}=\Delta\text{OH}_2\text{C}\).
[Nhớ vẽ hình đẹp, đầy đủ, trình bày rõ ràng]

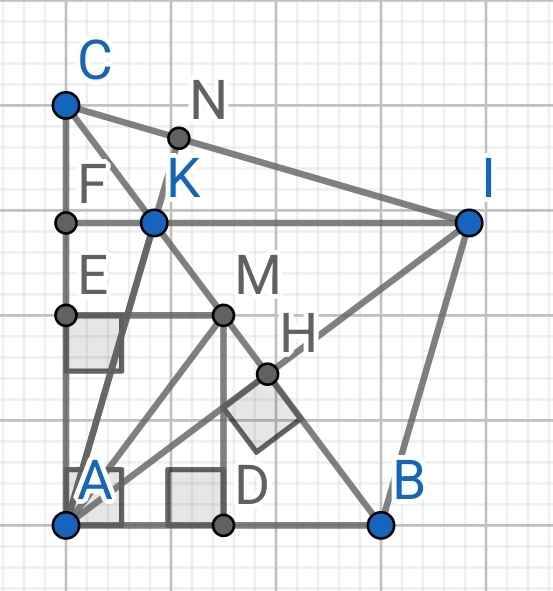
Giải: