Bài 27. Cho ΔABC vuông tại C có goc A=60 do . Tia phân giác của góc BAC cắt BC ở E. Kẻ BD vuông góc với tia AE (D AE). a) Chứng minh AD = BC. b) Kẻ EK vuông góc với AB (K ∈ AB). Chứng minh ΔAEB cân, từ đó suy ra AK = KB. c) Chứng minh: ba đường thẳng AC, EK, DB đồng qui.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 5 2023
a: Xét ΔACE vuông tại C và ΔAKE vuông tại K có
AE chung
góc CAE=góc KAE
=>ΔACE=ΔAKE
b: Xét ΔEAB có góc EAB=góc EBA
nên ΔEAB cân tại E
=>EA=EB
Xét ΔECA vuông tại C và ΔEDB vuông tại D có
EA=EB
góc AEC=góc BED
=>ΔECA=ΔEDB
=>EC=ED
=>AD=BC
6 tháng 2 2022
a)Vì AE là phân giác của góc BAC nên góc EAB=góc EBA
=> tg EAB cân tại E mà có EK là đg cao nên EK đồng thời là trung tuyên nên AK=BK
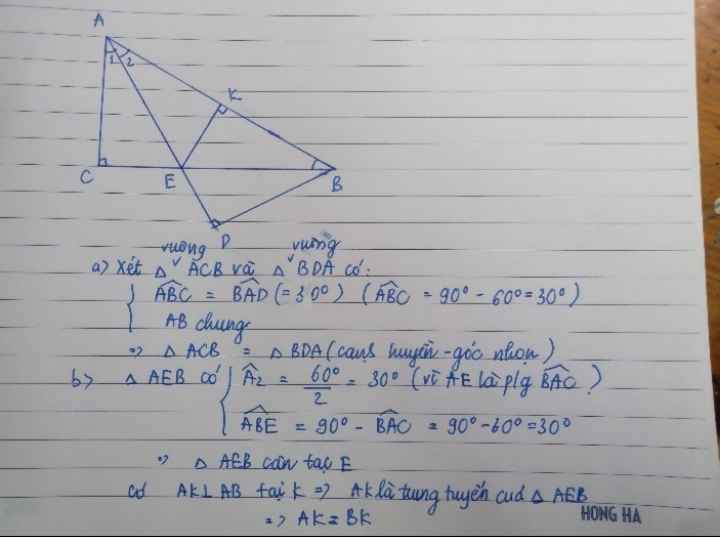
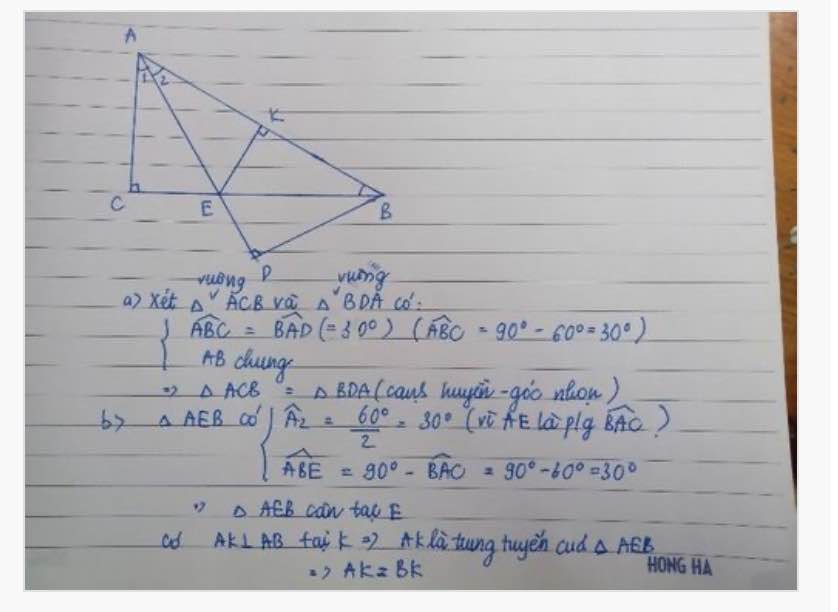
b)Xét tg ABC vuông tại C và tg BAD vuông tại D có
AB chung
ABC=BAD=30 độ
=> tg BAD=tg ABC(ch-gn)
=>AD=BC
CH
Cô Hoàng Huyền
Admin
VIP
26 tháng 2 2018
Em tham khảo tại đây nhé.
Câu hỏi của Bảo Trân Nguyễn Hoàng - Toán lớp 7 - Học toán với OnlineMath
b) Xét tam giác vuông ACB và tam giác vuông BDA có:
Cạnh AB chung
\(\widehat{ABC}=\widehat{BAD}\left(=30^o\right)\)
\(\Rightarrow\Delta ACB=\Delta BDA\) (Cạnh huyền góc nhọn)
\(\Rightarrow AD=BC\)
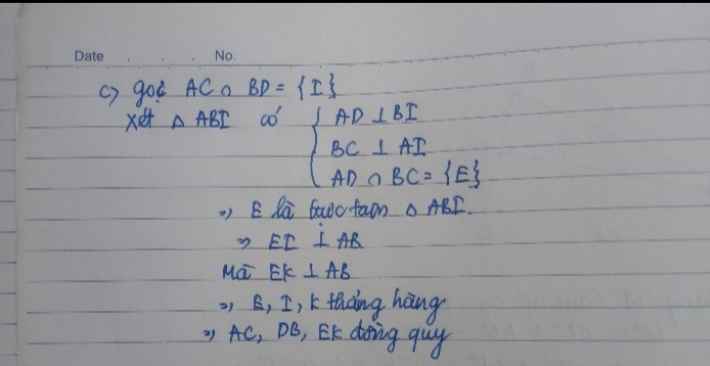
a, có AE là pg của ^BAC (gt) ; ^BAC = 60 (gt) => ^DAB = 30
xét tam giác ABC vuông tại C (gt) có ^BAC = 60 (gt) => ^CBA = 30
=> ^DAB = ^CBA
xét tam giác BDA và tam giác ACB có : AB chung
^BDA = ^ACB = 90
=> tam giác BDA = tam giác ACB (ch-gn)
=> AD = BC (Đn)
b, có : ^CBA = ^DAB = 30 (câu a)
=> tam giác BEA cân tại E (dh)
có EK là đường cao (gt)
=> EK đồng thời là đường trung tuyến của tam giác BEA (đl)
=> K là trung điểm của AB (đn)
=> BK = AK (đn)
c, kẻ BD cắt CA tại M
xét tam giác BMA có : AE _|_ BD ; BE _|_ CA; EK _|_ AB
=> AC;EK;BD đồng quy
ban oi dn va dh viet tat tu j v