giải bpt x4-8x3+23x2-28x+12<_0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TU
1
28 tháng 8 2021
Ta có: \(x^4-8x^3+21x^2-24x+9=0\)
\(\Leftrightarrow x^4-5x^3+3x^2-3x^3+15x^2-9x+3x^2-5x+9=0\)
\(\Leftrightarrow\left(x^2-5x+3\right)\left(x^2-3x+3\right)=0\)
\(\Leftrightarrow x^2-5x+3=0\)
\(\text{Δ}=\left(-5\right)^2-4\cdot1\cdot3=25-12=13\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{5-\sqrt{13}}{2}\\x_2=\dfrac{5+\sqrt{13}}{2}\end{matrix}\right.\)
HN
1
ST
2
19 tháng 8 2016
a) |x|+|y|=0 => x = 0 ; y = 0
ok nha!! 45434364565475675686875654645745745745745634564
CM
20 tháng 8 2019
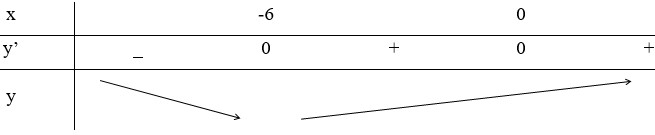
Đáp án B
y ' = 4 x 3 + 24 x 2 < 0 ⇔ 4 x 2 x + 6 < 0 ⇔ x < − 6 ⇒ hàm số nghịch biến trên − ∞ ; − 6
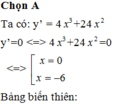
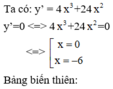
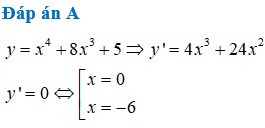
\(\Leftrightarrow x^4-4x^3+4x^2-4x^3+16x^2-16x+3x^2-12x+12\le0\)
\(\Leftrightarrow x^2\left(x^2-4x+4\right)-4x\left(x^2-4x+4\right)+3\left(x^2-4x+4\right)\le0\)
\(\Leftrightarrow\left(x^2-4x+3\right)\left(x-2\right)^2\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x^2-4x+3\le0\end{matrix}\right.\) \(\Rightarrow1\le x\le3\)