
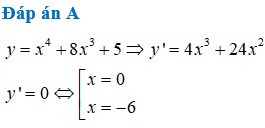
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

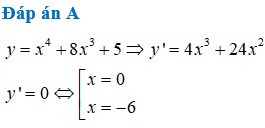


Đáp án A. Theo quy luật : cứ sau vòng lặp 2 số (vd 7-8) thì số thứ nhất giảm đi 1 đơn vị (vd 7->6) và số thứ 2 tăng lên 1 đơn vị (vd 8->9)

Đáp án C.
Ta có
f 2 − x ' = f ' 2 − x . 2 − x ' = − f ' 2 − x > 0 ⇔ f ' 2 − x < 0
Dựa vào đồ thị ta có:
f ' 2 − x < 0 ⇔ 2 − x < − 1 1 < 2 − x < 4 ⇔ x > 3 − 2 < x < 1
Vậy hàm số đồng biến trên − 2 ; 1 .

a) Theo đề bài, ta có :
\(\frac{5}{x}-\frac{y}{3}=\frac{1}{6}\) => \(\frac{5}{x}=\frac{1+2y}{6}\)
| 2y+1 | 1 | -1 | 3 | -3 | 5 | -5 | 15 | -15 |
| 2y | 0 | -2 | 2 | -4 | 4 | -6 | 14 | -16 |
| y | 0 | -1 | 1 | -2 | 2 | -3 | 7 | -8 |
| x | 30 | -30 | 10 | -10 | 6 | -6 | 2 | -2 |
b) \(\frac{2}{y}-\frac{x}{6}=\frac{1}{30}\) => \(\frac{2}{y}=\frac{5x-1}{30}\)
| 5x-1 | -1 | 4 | -6 |
| 5x | 0 | 5 | -5 |
| x | 0 | 1 | -1 |
| y | -60 | 15 | -10 |

Chọn A
Theo giả thiết ta có f’(x)≥0, (dấu bằng xảy ra tại hữu hạn điểm thuộc (a; b)).
Trên khoảng (a; b)
- Hàm số y = f(x)+1 có đạo hàm bằng f’(x) nên C đúng.
- Các hàm số y = - f(x)+1 và y = - f(x)-1 có đạo hàm bằng -f’(x) nên B, D đúng.
Do đó A sai

Ta có: Hàm số y=f(x) đồng biến trên khoảng a ; b ⇔ f ' ( x ) ≥ 0 , ∀ x ∈ a ; b , chỉ bằng 0 tại hữu hạn điểm trên (a;b).
+) Hàm số y=f(x)+1 có y ' = f ' ( x ) ≥ 0 , ∀ x ∈ ( a ; b ) , chỉ bằng 0 tại hữu hạn điểm trên (a;b).
⇒ y = f ( x ) + 1 đồng biến trên (a;b).
+) Hàm số y=-f(x) có y ' = - f ' ( x ) ≤ 0 , ∀ x ∈ ( a ; b ) , chỉ bằng 0 tại hữu hạn điểm trên (a;b).
⇒ y = - f ( x ) nghịch biến trên (a;b).
+) Hàm số y=-f(x)-1 có y ' = - f ' ( x ) ≤ 0 , ∀ x ∈ ( a ; b ) , chỉ bằng 0 tại hữu hạn điểm trên (a;b).
⇒ y = - f ( x ) - 1 nghịch biến trên (a;b).
+) Hàm số y=f(x+1) có y ' = f ' ( x + 1 ) : không có nhận xét về dấu dựa vào hàm số y=f(x)
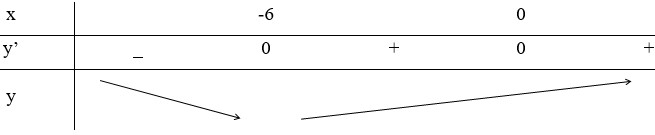
Chọn đáp án A.