\(3x^2-5x+m-2\)=0
Tim tổng và tich 2 nghiệm x1, x2 của phương tình trên theo m
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 4 2022
a.
\(\Delta=m^2-4\left(2m-4\right)=m^2-8m+16=\left(m-4\right)^2\ge0;\forall m\)
\(\Rightarrow\) Phương trình đã cho luôn có nghiệm với mọi m
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=2m-4\end{matrix}\right.\)
c.
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow m^2-2\left(2m-4\right)=4\)
\(\Leftrightarrow m^2-4m+4=0\Rightarrow m=2\)
7 tháng 4 2022
a.\(\Delta=m^2-4\left(2m-4\right)=m^2-8m+16=\left(m-4\right)^2\ge0\)
=> pt luôn có nghiệm với mọi m
b.Theo hệ thức Vi-ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1.x_2=2m-4\end{matrix}\right.\)
c.\(x_1^2+x_2^2=4\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2=4\)
\(\Leftrightarrow\left(-m\right)^2-2\left(2m-4\right)=4\)
\(\Leftrightarrow m^2-4m+8-4=0\)
\(\Leftrightarrow m^2-4m+4=0\)
\(\Leftrightarrow\left(m-2\right)^2=0\)
\(\Leftrightarrow m=2\)
KQ
1
14 tháng 4 2020
pt có 2 nghiệm x1, x2\(\Leftrightarrow\Delta\ge0\)
\(\Leftrightarrow25-12\left(m-2\right)\ge0\Leftrightarrow25-12m+24\ge0\Leftrightarrow49-12m\ge0\)
\(\Leftrightarrow m\le\frac{12}{49}\)
CM
10 tháng 1 2019
Phương trình (2m - 1) x 2 - 2(m + 4)x + 5m + 2 = 0 ( m ≠ 1 2 )
7 tháng 3 2021
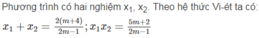
Theo hệ thức Vi-ét:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{5}{3}\left(1\right)\\x_1x_2=\dfrac{m}{3}\left(2\right)\end{matrix}\right.\)
Ta có \(6x_1+x_2=0\)\(\Rightarrow5x_1+\left(x_1+x_2\right)=0\Rightarrow5x_1+\dfrac{5}{3}=0\Leftrightarrow x_1=-\dfrac{1}{3}\) Thay vào (1) ta được:
\(x_2-\dfrac{1}{3}=\dfrac{5}{3}\Rightarrow x_2=2\)
Thay \(x_1=-\dfrac{1}{3};x_2=2\) vào (2) ta được:
\(-\dfrac{2}{3}=\dfrac{m}{3}\Rightarrow m=-2\)
\(S=\frac{5}{3}\)
\(P=\frac{m-2}{3}\)