Qua đồ thị hàm số \(y=x^2\)hãy cho biết khi x tăng từ \(-3\) đến \(2\) thì GTLN và GTNN của \(y\) là bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Lập bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = -0,75x2 | -12 | -3 | 0 | -3 | -12 |
- Vẽ đồ thị:
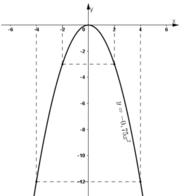
- Quan sát đồ thị hàm số y = -0,75x2:
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.

- Lập bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = - 0 , 75 x 2 | -12 | -3 | 0 | -3 | -12 |
- Vẽ đồ thị:
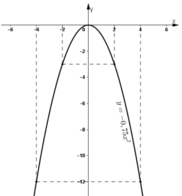
- Quan sát đồ thị hàm số y = - 0 , 75 x 2 :
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.

Vẽ đồ thị: y = -0,75x2
| x | -4 | -2 | -1 | 0 | 1 | 2 | 4 |
| y=-0,75x2 | -12 | -3 | -0,75 | 0 | -0,75 | -3 | -12 |
Vì -2 < 0 < 4 và khi x = 0 thì y = 0 là giá trị lớn nhất của hàm số. Hơn nữa khi x = -2 thì y = -0,75 . (-2)2 = -3, khi x = 4 thì y = -0,75 . (4)2 = -12 < -3
Do đó khi -2 ≤ x ≤ 4 thì giá trị nhỏ nhất của hàm số là -12 còn giá trị lớn nhất là 0.


Công thức biểu diễn diện tích y theo x là y = 3x vì với mỗi giá trị của x ta xác định được chỉ một giá trị tương ứng của y nên đại lượng là hàm số của đại lượng x.
Cho x = 1 được y = 3 => A(1;3) thuộc đồ thị.
Vẽ đồ thị: Hình dưới
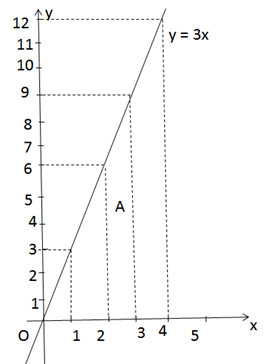
a) Trên đồ thị thấy: x = 3 => y = 9. Vậy khi x = 3 thì diện tích hình chữ nhật bằng 9 (m2).
x = 4 => y = 12 . Vậy khi x = 4 thì diện tích hình chữ nhật bằng 12 (m2).
b) y = 6 => x = 2. Vậy khi diện tích hình chữ nhật bằng 6 thì cạnh x = 2 (m).
y = 9 => x = 3. Vậy diện tích hình chữ nhật bằng 9 thì cạnh x = 3 (m)
Ta có đồ thị hàm số $y=x^2$
Suy ra Giá trị lớn nhất trong đoạn từ $-3$ đến $2$ là $9$ khi $x=-3$
Giá trị nhỏ nhất trong đoạn từ $-3$ đến $2$ là $0$ khi \(x=0\)