Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
a) a = -2.
b) Ta có 7 = a . 2 + 3. Suy ra a = 2.

a:
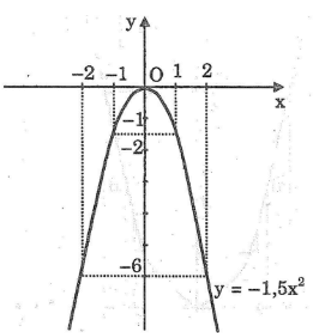
b: Vì a=-1,5<0 nên hàm số đồng biến khi x<0 và nghịch biến khi x>0
=>f(-1,5)< f(-0,5) và f(0,75)>f(1,5)
- Khi 1 ≤ x ≤ 2 thì -6 ≤ y ≤ -1,5 ;
- Khi -2 ≤ x ≤ 0 thì -6 ≤ y ≤ 0 ;
- Khi -2 ≤ x ≤ 1 thì -6 ≤ y ≤ 0.

a) Vì đồ thị hàm số đi qua A(1;-1) nên ta có :
x= 1 ; y=-1 và thay vào hàm số ta có
y= (2a+3) <=> -1 = (2a + 3)*1 <=> 2a + 3 = -1 <=> 2a = - 3 - 1 <=> 2a = -4 <=> a = -2
Vậy đồ thị hàm số có dạng y = ( -4 +3)x = -1x
- Ta có phương trình hoành độ giao điểm :
-1x = 4x - 5
<=> -1x - 4x = -5
<=>-5x = -5 <=> x = 1 => y = -1x = -1 * 1 = -1
Vậy 2 đồ thị hàm số giao nhau tại B ( 1; -1)
b) Vì hoành độ bằng 1 bằng 1 nên x = 1
Ta có phương trình hoành độ giao điểm :
(2a + 3 )x = -2x +2
thay x = 1 vào phương trình ta có :
( 2a + 3)*1 = -2*1 + 2
<=> 2a + 3 = -2+ 2
<=> 2a = -2 +2 -3 <=> a = \(-\frac{3}{2}\)

Ta có: \(\left(x-y\right)^2\ge0\)
\(\Leftrightarrow x^2-2xy+y^2\ge0\Rightarrow x^2+y^2\ge2xy\)
Tương tự: \(y^2+z^2\ge2yz\); \(x^2+z^2\ge2xz\)
Cộng từng vế của các BDDT trên:
\(2\left(xz+yz+xy\right)\le2\left(x^2+y^2+z^2\right)\)
\(\Leftrightarrow xy+yz+xz\le x^2+y^2+z^2\)
\(\Leftrightarrow3xy+3yz+3xz\le x^2+y^2+z^2+2xy+2yz+2xz\)
\(\Leftrightarrow3xy+3yz+3xz\le\left(x+y+z\right)^2\)
\(\Leftrightarrow3xy+3yz+3xz\le3^2=9\)
\(\Leftrightarrow xy+yz+xz\le3\)
Vậy \(D_{max}=3\Leftrightarrow x=y=z\)
Áp dụng BĐT Cauchy - Schwarz:
\(\left(x^2+y^2+z^2\right)\left(1+1+1\right)\)
\(=\left(x^2+y^2+z^2\right)\left(1^2+1^2+1^2\right)\ge\left(x+y+z\right)^2\)
\(\Rightarrow3\left(x^2+y^2+z^2\right)\ge3^2=9\)
\(\Rightarrow x^2+y^2+z^2\ge3\)
Vậy \(C_{min}=3\Leftrightarrow x=y=z=1\)

Ta có đồ thị hàm số $y=x^2$
Suy ra Giá trị lớn nhất trong đoạn từ $-3$ đến $2$ là $9$ khi $x=-3$
Giá trị nhỏ nhất trong đoạn từ $-3$ đến $2$ là $0$ khi \(x=0\)