Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn ấn vào đúng 0 sẽ ra kết quả, mình giải được rồi dễ lắm

Nếu x ≤ 1 thì f(x,y) ≤ 0 => f(x,y) lớn nhất là 0
Khi x = -y v x+1 = y ; x+1
- Mặt khác do : -x ≤ y ≤ x+1 => x+1 ≥ -x <=> x > \(-\frac{1}{2}\)
Vậy nếu \(-\frac{1}{2}\) < x < 1 thì ta có :
f(x,y) = \(\left(1-x\right)\sqrt{\left(x-y+1\right)\left(x+y\right)}\le\left(1-x\right)\frac{1}{2}\left(x-y+1+x+y\right)\)
f(x,y) = \(\left(1-x\right)\left(x+\frac{1}{2}\right)\le\frac{1}{4}\left(1-x+x+\frac{1}{2}\right)^2=\frac{9}{16}\)
Vậy f(x,y) lớn nhất là \(\frac{9}{16}\)khi x=\(\frac{1}{4}\)và y=\(\frac{1}{2}\)

Một cửa hàng ngày thứ nhất bán 180 tạ gạo, ngày thứ hai bán 270 tạ gạo , ngày thứ ba bán kém hơn ngày thứ hai một nửa .Hỏi trung bình mỗi ngày cửa hàng bán được bao nhiêu tạ gạo ?
1) Xét hiệu :
\(\left(x_1+x_2+x_3\right)\left(y_1+y_2+y_3\right)-3\left(x_1y_1+x_2y_2+x_3y_3\right).\)
\(=x_1\left(y_1+y_2+y_3\right)-3x_1y_1+x_2\left(y_1+y_2+y_3\right)-3x_2y_2+x_3\left(y_1+y_2+y_3\right)-3x_3y_3.\)
\(=x_1\left(y_2+y_3-2y_1\right)+x_2\left(y_1+y_3-2y_2\right)+x_3\left(y_1+y_2-2y_3\right)\)
\(=x_1\left[\left(y_2-y_1\right)-\left(y_1-y_3\right)\right]+x_2\left[\left(y_3-y_2\right)-\left(y_2-y_1\right)\right]+x_3\left[\left(y_1-y_3\right)-\left(y_3-y_2\right)\right]\)
\(=\left(y_2-y_1\right)\left(x_1-x_2\right)+\left(y_1-y_3\right)\left(x_3-x_1\right)+\left(y_3-y_2\right)\left(x_2-x_3\right)\le0\)
Vì \(x_1\le x_2\le x_3;y_1\le y_2\le y_3\)

Bài 3: \(A=\frac{\left(2a+b+c\right)\left(a+2b+c\right)\left(a+b+2c\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
Đặt a+b=x;b+c=y;c+a=z
\(A=\frac{\left(x+y\right)\left(y+z\right)\left(z+x\right)}{xyz}\ge\frac{2\sqrt{xy}.2\sqrt{yz}.2\sqrt{zx}}{xyz}=\frac{8xyz}{xyz}=8\)
Dấu = xảy ra khi \(a=b=c=\frac{1}{3}\)
Bài 4: \(A=\frac{9x}{2-x}+\frac{2}{x}=\frac{9x-18}{2-x}+\frac{18}{2-x}+\frac{2}{x}\ge-9+\frac{\left(\sqrt{18}+\sqrt{2}\right)^2}{2-x+x}=-9+\frac{32}{2}=7\)
Dấu = xảy ra khi\(\frac{\sqrt{18}}{2-x}=\frac{\sqrt{2}}{x}\Rightarrow x=\frac{1}{2}\)
a: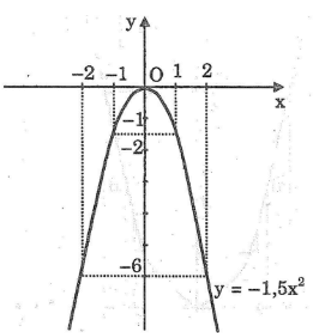
b: Vì a=-1,5<0 nên hàm số đồng biến khi x<0 và nghịch biến khi x>0
=>f(-1,5)< f(-0,5) và f(0,75)>f(1,5)
- Khi 1 ≤ x ≤ 2 thì -6 ≤ y ≤ -1,5 ;
- Khi -2 ≤ x ≤ 0 thì -6 ≤ y ≤ 0 ;
- Khi -2 ≤ x ≤ 1 thì -6 ≤ y ≤ 0.