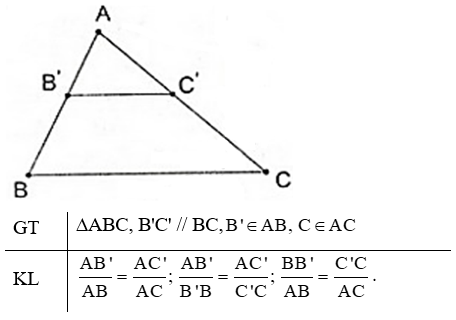
Nhắc lại định lý Ta-lét trong tam giác.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 4 2017
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ
SG
1
2 tháng 3 2022
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Đề sai rồi bạn
TC
28 tháng 10 2018
Tam giác ABC có MN // BC (M thuộc AB, N thuộc AC)
S(ACM)/S(ABC) = AM/AB (1)
S(ABN)/S(ABC) = AN/AC (2)
Mà S(ACM) = S(AMN) + S(CMN) (3)
và S(ABN) = S(AMN) + SBMN) (4)
Mặt khác do MNCB hình thang nên dễ dàng chứng minh
S(CMN) = S(BMN) (5)
Từ (3) , (4) và (5) cho:
S(ACM) = S(ABN) (6)
(1) , (2) và (6) cho:
AM/AB = AN/AC (đpcm)
-----------
Cách viết S(ABC) đọc là diện tích tam giác ABC
CM
10 tháng 5 2019
Định lí Cô sin : Tam giác ABC có AB = c, BC = a, AC = c thì ta có :
PT
30 tháng 3 2017
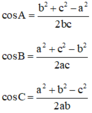
Định lí:
Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.
Ta có các hệ thức sau: a2 = b2 + c2 - 2bc.cosA (1)
b2 = a2 + c2 - 2bc.cosB (2)
c2 = a2 + b2 - 2bc.cosC (3)
Hệ quả: Từ định lí cosin suy ra:
cosA = cosB =
cosC =