Giải bất phương trình:
(x+3).Căn(x2-4)<=x2-9
Giúp e với ạ :((
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 5 2023
Δ=(2m-6)^2-4(m^2+3)
=4m^2-24m+36-4m^2-12=-24m+24
Để phương trình có hai nghiệm phân biệt thì -24m+24>0
=>m<1
x1^2+x2^2=36
=>(x1+x2)^2-2x1x2=36
=>(2m-6)^2-2(m^2+3)=36
=>4m^2-24m+36-2m^2-6-36=0
=>2m^2-24m-6=0
=>m^2-12m-3=0
=>\(m=6-\sqrt{39}\)
NN
2
Y
11 tháng 4 2022
\(x^2-2x+1< 9\)
\(\Leftrightarrow\left(x-1\right)^2< 9\)
\(\Leftrightarrow x-1< 3\)
\(\Leftrightarrow x< 4\)
\(\left(x-1\right)\left(4-x^2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2-x\right)\left(2+x\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2-x=0\\2+x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-2\end{matrix}\right.\)
\(\dfrac{x+2}{x-5}< 0\)
\(\Leftrightarrow x+2< 0\)
\(\Leftrightarrow x< -2\)
11 tháng 4 2022
a)\(x^2-2x+1< 9\)
\(\Leftrightarrow\left(x-1\right)^2< 9\)
\(\Leftrightarrow\left(x-1\right)^2-9< 0\)
\(\Leftrightarrow\left(x-1-3\right)\left(x-1+3\right)< 0\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4< 0\\x+2>0\end{matrix}\right.hay\left[{}\begin{matrix}x-4>0\\x+2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 4\\x>-2\end{matrix}\right.hay\left[{}\begin{matrix}x>4\\x< -2\end{matrix}\right.\)(vô lý)
-Vậy nghiệm của BĐT là \(-2< x< 4\).
b) \(\left(x-1\right)\left(4-x^2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2-x\right)\left(x+2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x+2\right)\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1< 0\\x-2>0\\x+2>0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1>0\\x-2< 0\\x+2>0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1>0\\x-2 >0\\x+2< 0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1< 0\\x-2< 0\\x+2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 1\\x>2\\x>-2\end{matrix}\right.\) (vô lí) hay \(\left[{}\begin{matrix}x>1\\x< 2\\x>-2\end{matrix}\right.\) (có thể xảy ra) hay
\(\left[{}\begin{matrix}x>1\\x>2\\x< -2\end{matrix}\right.\) (vô lí) hay \(\left[{}\begin{matrix}x< 1\\x< 2\\x< -2\end{matrix}\right.\) (có thể xảy ra)
-Vậy nghiệm của BĐT là \(x< -2\) hay \(1< x< 2\).
c) ĐKXĐ: \(x\ne5\)
\(\dfrac{x+2}{x-5}< 0\Leftrightarrow\left[{}\begin{matrix}x+2< 0\\x-5>0\end{matrix}\right.hay\left[{}\begin{matrix}x+2>0\\x-5< 0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x< -2\\x>5\end{matrix}\right.\)(vô lí) hay
\(\left[{}\begin{matrix}x>-2\\x< 5\end{matrix}\right.\) (có thể xảy ra)
-Vậy nghiệm của BĐT là \(-2< x< 5\)
10 tháng 5 2023
=>căn 2x1=x2-1
=>2x1=x2^2-2x2+1
=>x2^2-2(x1+x2)+1=0
=>x2^2-2(2m+1)+1=0
=>x2^2=4m+2-1=4m+1
=>\(x_2=\pm\sqrt{4m+1}\)
=>\(x_1=2m+1\pm\sqrt{4m+1}\)
x1*x2=m^2-m
=>m^2-m=4m+1\(\pm2m+1\)
=>m^2-5m-1=\(\pm2m+1\)
TH1: m^2-5m-1=2m+1
=>m^2-7m-2=0
=>\(m=\dfrac{7\pm\sqrt{57}}{2}\)
TH2: m^2-5m-1=-2m-1
=>m^2-3m=0
=>m=0; m=3
PT
20 tháng 3 2022
a) x(4x + 2) = 4x2 - 14
⇔ 4x2 + 2x = 4x2 - 14
⇔ 4x2 - 4x2 + 2x = -14
⇔ 2x = -14
⇔ x = -7
Vậy tập nghiệm S = ......
b) (x2 - 9)(2x - 1) = 0
⇔ x2 - 9 = 0 hoặc 2x - 1 = 0
⇔ x2 = 9 hoặc 2x = 1
⇔ x = 3 hoặc -3 hoặc x = \(\dfrac{1}{2}\)
Vậy .......
c) \(\dfrac{3}{x-2}\) + \(\dfrac{4}{x+2}\) = \(\dfrac{x-12}{x^2-4}\)
⇔ \(\dfrac{3}{x-2}\) + \(\dfrac{4}{x+2}\) = \(\dfrac{x-12}{\left(x-2\right)\left(x+2\right)}\)
ĐKXĐ: x - 2 ≠ 0 và x + 2 ≠ 0
⇔ x ≠ 2 và x ≠ -2MSC (mẫu số chung): (x - 2)(x + 2)Quy đồng mẫu hai vế và khử mẫu ta được:3x + 6 + 4x - 8 = x - 12⇔ 3x + 4x - x = 8 - 6 - 12⇔ 6x = -10⇔ x = \(-\dfrac{5}{3}\) (nhận)Vậy ........
CM
21 tháng 2 2018
Đáp án: A
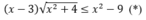
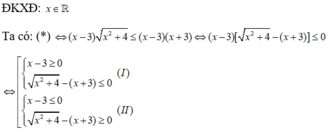
Giải (I):
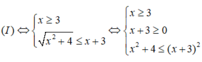
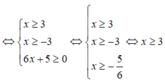
Giải (II):
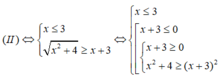
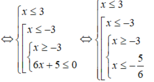
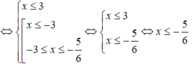
Vậy tập nghiệm của bất phương trình đã cho là:
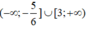
biến đổi tương đương (x+3)(\(\sqrt{x^2-4}-x-3\))≤0
TH1 :
\(\left\{{}\begin{matrix}\sqrt{x^2-4}-x-3\text{>=0}\\\text{x+3≤0}\end{matrix}\right.\)
trường hợp 2 thì ngược với trường hợp 1 nếu bạn học lớp 10 rồi chắc đây đây là biết