Cho tam giác ABC cân tại A có A= 110 độ . Trên cạnh BC lấy điểm D và E sao cho BD = BA , CE = CA .
Tính số đo góc DAE
( Giải bằng 2 cách )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

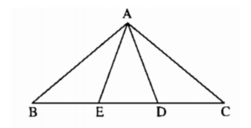
+) Ta có:
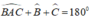 (tổng ba góc trong 1 tam giác)
(tổng ba góc trong 1 tam giác)
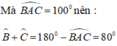
Lại có: tam giác ABC là tam giác cân tại A nên:
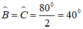
+)Xét tam giác ABD có BA= BD (giả thiết) nên tam giác ABD cân tại B.
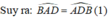
Lại có; 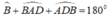 ( tổng ba góc trong 1 tam giác)
( tổng ba góc trong 1 tam giác)
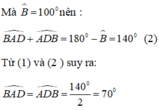
+) Tương tự, ta có tam giác AEC cân tại C ( vì CA =CE)
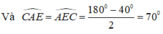
+) Xét tam giác ADE có:
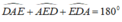 ( tổng ba góc trong tam giác)
( tổng ba góc trong tam giác)
Suy ra:
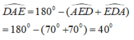

đừng tích ai nhá, tôi về mình giải cho, giờ mik phải đi học thêm

ΔABD cân tại B có = 50º nên
= 70º
ΔACE cân tại C có = 50º nên
= 70º
Answer:
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow100^o+\widehat{C}+\widehat{B}=180^o\)
\(\Rightarrow2\widehat{B}=80^o\)
\(\Rightarrow\widehat{B}=\widehat{C}=40^o\)
Ta có: Tam giác ACE cân tại C
Mà: \(\widehat{A}+\widehat{C}+\widehat{E}=180^o\)
\(\Rightarrow2\widehat{E}+40^o=180^o\)
\(\Rightarrow2\widehat{E}=140^o\)
\(\Rightarrow\widehat{E}=70^o\) (1)
Ta có: Tam giác ABD cân tại B
Mà: \(\widehat{A}+\widehat{B}+\widehat{D}=180^o\)
\(\Rightarrow2\widehat{D}+40^o=180^o\)
\(\Rightarrow2\widehat{D}=140^o\)
\(\Rightarrow\widehat{D}=70^o\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{A}+\widehat{E}+\widehat{D}=180^o\)
\(\Rightarrow\widehat{A}+2.70^o=180^o\)
\(\Rightarrow\widehat{A}+140^o=180^o\)
\(\Rightarrow\widehat{A}=40^o\)
Vậy \(\widehat{DAE}=40^o\)

ΔABD cân tại B có = 50º nên
= 70º
ΔACE cân tại C có = 50º nên
= 70º
Mk bận ko vẽ hình được thông cảm :
+ Vì ΔABCΔABC cân tại A(gt)A(gt)
=> Bˆ=CˆB^=C^ (tính chất tam giác cân).
=> Bˆ=Cˆ=1800−Aˆ2B^=C^=1800−A^2
=> Bˆ=Cˆ=1800−11002=7002=350.B^=C^=1800−11002=7002=350.
+ Xét ΔABDΔABD có:
BD=BA(gt)BD=BA(gt)
=> ΔABDΔABD cân tại B.
=> BADˆ=ADBˆBAD^=ADB^ (tính chất tam giác cân).
=> BADˆ=ADBˆ=1800−Bˆ2BAD^=ADB^=1800−B^2
=> BADˆ=ADBˆ=1800−3502=14502=72,50.BAD^=ADB^=1800−3502=14502=72,50.
=> ADBˆ=72,50ADB^=72,50
Hay ADEˆ=72,50.ADE^=72,50.
+ Xét ΔACEΔACE có:
CE=CA(gt)CE=CA(gt)
=> ΔACEΔACE cân tại C.
=> CAEˆ=AECˆCAE^=AEC^ (tính chất tam giác cân).
=> CAEˆ=AECˆ=1800−Cˆ2CAE^=AEC^=1800−C^2
=> CAEˆ=AECˆ=1800−3502=14502=72,50.CAE^=AEC^=1800−3502=14502=72,50.
=> AECˆ=72,50AEC^=72,50
Hay AEDˆ=72,50.AED^=72,50.
+ Xét ΔADEΔADE có:
DAEˆ+ADEˆ+AEDˆ=1800DAE^+ADE^+AED^=1800 (định lí tổng 3 góc trong một tam giác).
=> DAEˆ+72,50+72,50=1800DAE^+72,50+72,50=1800 => DAEˆ+1450=1800DAE^+1450=1800 => DAEˆ=1800−1450DAE^=1800−1450 => DAEˆ=350.DAE^=350. Vậy DAEˆ=350.DAE^=350. Chúc bạn học tốt!
+ Vì ΔABCΔABC cân tại A(gt)A(gt)
=> Bˆ=CˆB^=C^ (tính chất tam giác cân).
=> Bˆ=Cˆ=1800−Aˆ2B^=C^=1800−A^2
=> Bˆ=Cˆ=1800−11002=7002=350.B^=C^=1800−11002=7002=350.
+ Xét ΔABDΔABD có:
BD=BA(gt)BD=BA(gt)
=> ΔABDΔABD cân tại B.
=> BADˆ=ADBˆBAD^=ADB^ (tính chất tam giác cân).
=> BADˆ=ADBˆ=1800−Bˆ2BAD^=ADB^=1800−B^2
=> BADˆ=ADBˆ=1800−3502=14502=72,50.BAD^=ADB^=1800−3502=14502=72,50.
=> ADBˆ=72,50ADB^=72,50
Hay ADEˆ=72,50.ADE^=72,50.
+ Xét ΔACEΔACE có:
CE=CA(gt)CE=CA(gt)
=> ΔACEΔACE cân tại C.
=> CAEˆ=AECˆCAE^=AEC^ (tính chất tam giác cân).
=> CAEˆ=AECˆ=1800−Cˆ2CAE^=AEC^=1800−C^2
=> CAEˆ=AECˆ=1800−3502=14502=72,50.CAE^=AEC^=1800−3502=14502=72,50.
=> AECˆ=72,50AEC^=72,50
Hay AEDˆ=72,50.AED^=72,50.
+ Xét ΔADEΔADE có:
DAEˆ+ADEˆ+AEDˆ=1800DAE^+ADE^+AED^=1800 (định lí tổng 3 góc trong một tam giác).
=> DAEˆ+72,50+72,50=1800DAE^+72,50+72,50=1800 => DAEˆ+1450=1800DAE^+1450=1800 => DAEˆ=1800−1450DAE^=1800−1450 => DAEˆ=350.DAE^=350. Vậy DAEˆ=350.DAE^=350.
Chúc bạn học tốt!