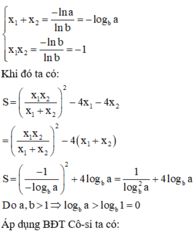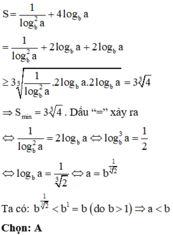Giá trị nào sau đây không là nghiệm của bất phương trình 4x2−9<2x4x2
A. x=\(\frac{1}{2}\)
B. x=1
C. x=\(\frac{3}{2}\)
D. x=2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thử x = -1 vào các bất phương trình ta thấy x = -1 là nghiệm của bất phương trình 2x + 1 < 0.
Cũng có thể giải các bất phương trình, từ đó thấy x = -1 chỉ là nghiệm của phương trình 2x + 1 < 0. Đáp án là B.

(Trong bài này chúng ta làm theo cách thứ 2) thay x = 2 vào từng bất phương trình:
Đáp án A: 7 – 2 < 2.2 ó 5 < 4 vô lý. Loại đáp án A.
Đáp án B: 2.2 + 3 > 9 ó 7 > 9 vô lý. Loại đáp án B
Đáp án C: -4.2 ≥ 2 + 5 ó -8 ≥ 7 vô lý. Loại đáp án C.
Đáp án D: 5 – 2 > 6.2 ó 3 > 0 luôn đúng. Chọn đáp án D
Đáp án cần chọn là: D

Thay x= 3 vào các bất phương trình ta thấy x= 3 chỉ thỏa mãn bất phương trình 2x – 1 > 3.
Chọn D.

Cách 1: Điều kiện xác định của bất phương trình là x < 3. Khi đó:
1 - x 3 - x > x - 1 3 - x ⇔ 1 - x > x - 1 ⇔ x - 1 < 0 ⇔ x < 1 .
Kết hợp lại, suy ra nghiệm của bất phương trình đã cho là x < 1.
Đáp án là C.
Cách 2: Có thể thay các giá trị trên vào bất phương trình, thực chất chỉ cần thay vào x - 1 ( bỏ đi) rồi suy ra kết luận.

Thay x = 3 lần lượt vào từng vế của mỗi bất phương trình, ta được:
a) 2x + 3 = 2.3 + 3 = 9
Vậy x = 3 không là nghiệm của bất phương trình 2x + 3 < 9.
b) -4x = -4.3 = -12
2x + 5 = 2.3 + 5 = 11
-12 < 11 nên x = 3 không phải nghiệm của bất phương trình -4x > 2x + 5.
c) 5 – x = 5 – 3 = 2
3x – 12 = 3.3 – 12 = -3.
Vì 2 > -3 nên x = 3 là nghiệm của bất phương trình 5 – x > 3x – 12.

Chọn C.
Ta có: m(x - m) ≤ x - 1 ⇔ mx - m 2 ≥ x - 1 ⇔ (m - 1)x ≥ m 2 - 1
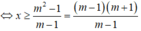
+) Với m < 1 ⇒ m – 1 < 0 ⇒ Tập nghiệm của bất phương trình là S = ( - ∞ ;m+1].
+) Với m > 1 ⇒ m – 1 > 0 ⇒ Tập nghiệm của bất phương trình là S = [m+1; + ∞ ).

Phương pháp:
+) Lấy loganepe hai vế, đưa phương trình về dạng phương trình bậc hai ẩn x.
+) Tìm điều kiện để phương trình có 2 nghiệm. Áp dụng định lí Vi-ét.
+) Sử dụng BĐT Cô-si cho 3 số không âm đánh giá biểu thức S.
Cách giải: