Cho hàm số : y = 2x\(^2\) (P) . Viết phương trình đường thẳng đi qua điểm (0;-2) và tiếp xúc với (P)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


phương trình của đt là y=ax+b
vì d đi qua điểm (0,-2) nên thay x=0,y=-2 vào pt
-2=0a+b
b=-2
vậy phương trình đt là y=ax-2

Thay x=2 vào (P), ta được:
y=1/2*2^2=1/2*4=2
(d): y=ax+b đi qua A(0;-2) và B(2;2) nên ta có hệ phương trình:
0a+b=-2 và 2a+b=2
=>b=-2 và 2a=4
=>a=2 và b=-2
=>y=2x-2

a: Thay x=1 và y=1 vào (d), ta được:
m+3=1
hay m=-2
b: Vì (d)//y=-2x+3 nên a=-2
Vậy: (d): y=-2x+b
Thay x=0 và y=-3 vào (d), ta được:
b=-3

a: Thay x=1 và y=1 vào (d), ta được:
m+3=1
hay m=-2
b: Vì (d)//y=-2x+3 nên a=-2
Vậy: (d): y=-2x+b
Thay x=0 và y=-3 vào (d), ta được:
b=-3

b. PTHĐGĐ của hai hàm số:
\(x+2=-2x+1\)
\(\Rightarrow x=-\dfrac{1}{3}\)
Thay x vào hs đầu tiên: \(y=-\dfrac{1}{3}+2=\dfrac{5}{3}\)
Tọa độ điểm \(A\left(-\dfrac{1}{3};\dfrac{5}{3}\right)\)
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2=-2x+1\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)

gọi pt đt d cần tìm là: y=ax+b
vì d đi qua M(0;-2) nên ta thay x=0, y=-2 vào d: \(-2=0a+b\Leftrightarrow b=-2\)=> (d): y=ax-2
xét pt: \(2x^2=ax-2\Leftrightarrow2x^2-ax+2=0\); \(\Delta=1-4.2.2=-15<0\Rightarrow\)d và P k giao nhau
=> k tìm đc đt d t/m
hình như đề sai bạn ạ. vì k tìm đc d nên câu b k làm đc luôn

\(b,\text{PT hoành độ giao điểm: }x+2=-2x+1\Leftrightarrow3x=-1\\ \Leftrightarrow x=-\dfrac{1}{3}\Leftrightarrow y=\dfrac{5}{3}\Leftrightarrow A\left(-\dfrac{1}{3};\dfrac{5}{3}\right)\\ c,\text{Gọi }y=ax+b\left(a\ne0\right)\text{ là đt cần tìm}\\ \Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne1\\-\dfrac{1}{3}a+b=\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=\dfrac{7}{3}\end{matrix}\right.\\ \Leftrightarrow y=2x+\dfrac{7}{3}\)

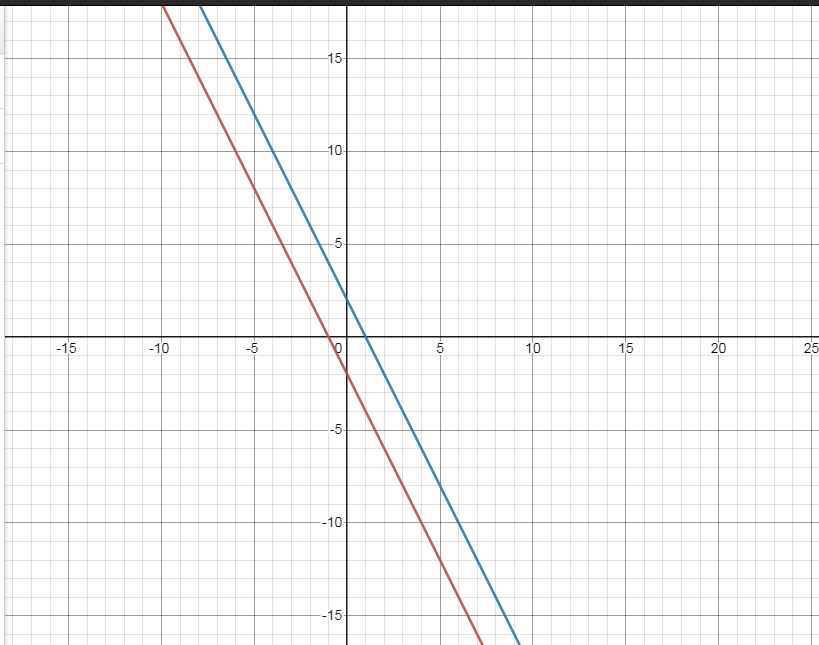
a) \(\left(d_1\right):y=-2x-2\)
\(\left(d_2\right):y=ax+b\)
\(\left(d_2\right)//d_1\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b\ne-2\end{matrix}\right.\)
\(\Leftrightarrow\left(d_2\right):y=-2x+b\)
\(M\left(2;-2\right)\in\left(d_2\right)\Leftrightarrow-2.2+b=-2\)
\(\Leftrightarrow b=2\) \(\left(thỏa.đk.b\ne-2\right)\)
Vậy \(\left(d_2\right):y=-2x+2\)
b) \(\left\{{}\begin{matrix}\left(d_1\right):y=-2x-2\\\left(d_2\right):y=-2x+2\end{matrix}\right.\)
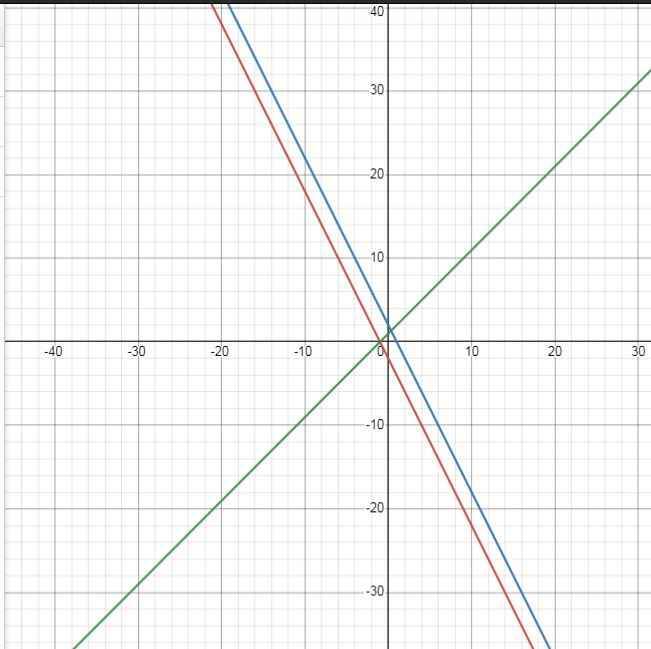
c) \(\left(d_3\right):y=x+m\)
\(\left(d_1\right)\cap\left(d_3\right)=A\left(x;0\right)\Leftrightarrow\left\{{}\begin{matrix}y=x+m\\y=-2x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}0=x+m\\0=-2x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\x=-1\end{matrix}\right.\)
\(\Rightarrow\left(d_3\right):y=x+1\)

Gọi phương trình đường thẳng (d) có dạng \(y=ax+b\)
(d) qua \(\left(0;-2\right)\Rightarrow-2=0.a+b\Rightarrow b=-2\Rightarrow y=ax-2\)
Phương trình hoành độ giao điểm (d) và (P):
\(2x^2=ax-2\Leftrightarrow2x^2-ax+2=0\) (1)
(d) tiếp xúc (P) \(\Leftrightarrow\left(1\right)\) có nghiệm kép
\(\Leftrightarrow\Delta=a^2-16=0\Rightarrow a=\pm4\)
Vậy có 2 pt đường thẳng thỏa mãn: \(\left[{}\begin{matrix}y=4x-2\\y=-4x-2\end{matrix}\right.\)