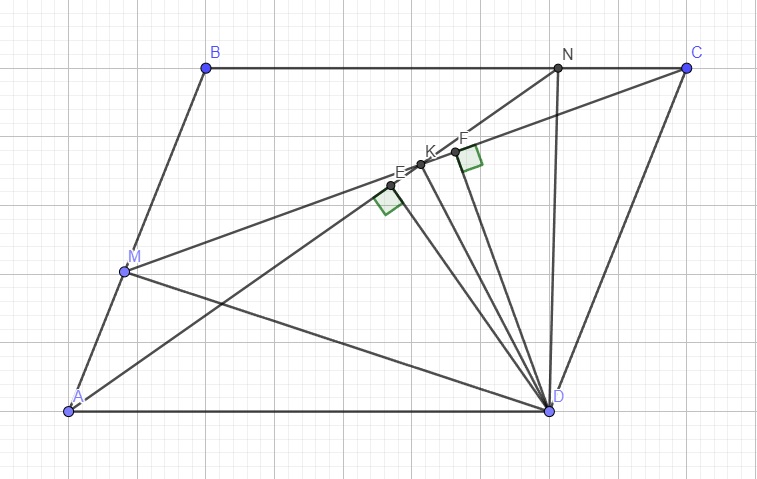
Cho hình vuông ABCD M là trung điểm cạnh BC. trên cạnh CD lấy điểm N sao cho NC=2ND. gọi K là giao điểm của AN với BD và O là tâm của hình vuông. Chứng minh KO=KD
Gọi E là trung điểm của OA chứng minh BE vuông góc với KA
Chúng minh KMN là tam giác vuông