giúp em bài 3 với ạ em cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: AD vuông góc CD
SA vuông góc CD
=>CD vuông góc (SAD)
Kẻ AH vuông góc SD
=>CD vuông góc AH
mà SD vuông góc AH
nên AH vuông góc (CDS)
=>d(A;(SCD))=AH=căn (4a^2+16a^2/8a^2)=căn 10/2
Kẻ MP//AB//CD
=>AP/AD=AM/AC
=>AP/4a=1/4
=>AP=a
=>PD=3a
PQ vuông góc SD
PQ vuông góc CD
=>PQ vuông góc (SCD)
mà PM//(SCD)
nên d(P;(SCD))=PQ
Xét ΔADH có PQ/AH=PD/AD
\(\dfrac{PQ}{\sqrt{10}:2}=\dfrac{3a}{4a}=\dfrac{3}{4}\)
=>PQ=3 căn 10/8
=>d(M;(SCD))=PQ=3căn 10/8
Kẻ NG//AM
Kẻ GU vuông góc SD
=>d(G;(SCD))=GU
GU/AH=SG/SA=1/2
=>GU=căn 10/4
b: (SCD;ABCD))=(AD;SD)=góc ADH
AH=AD*cosADH
=>cosADH=căn 10/8
=>góc ADH=67 độ
(SBD;(ABCD))=góc SOA
SA=AO*tan SOA
=>tan SOA=2/5
=>góc SOA=22 độ

a.
\(n_S=\dfrac{16}{32}=0,5mol\)
Gọi \(\left\{{}\begin{matrix}n_{Zn}=x\\n_{Mg}=y\end{matrix}\right.\)
\(Zn+S\rightarrow\left(t^o\right)ZnS\)
x x ( mol )
\(Mg+S\rightarrow\left(t^o\right)MgS\)
y y ( mol )
Ta có:
\(\left\{{}\begin{matrix}65x+24y=23,4\\x+y=0,5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{57}{205}\\y=\dfrac{91}{410}\end{matrix}\right.\)
\(\rightarrow\left\{{}\begin{matrix}m_{Zn}=\dfrac{57}{205}.65=\dfrac{741}{41}g\\m_{Mg}=\dfrac{91}{410}.24=\dfrac{1092}{205}g\end{matrix}\right.\)
\(\rightarrow\left\{{}\begin{matrix}\%m_{Zn}=\dfrac{741}{41}:23,4.100=77,23\%\\\%m_{Mg}=100\%-77,23\%=22,77\%\end{matrix}\right.\)
b.\(ZnS+2HCl\rightarrow ZnCl_2+H_2S\)
57/205 57/205 ( mol )
\(MgS+2HCl\rightarrow MgCl_2+H_2S\)
91/410 91/410 ( mol )
\(V_{H_2S}=\left(\dfrac{57}{205}+\dfrac{91}{410}\right).22,4=11,2l\)


Bài 2:
\(a,\Rightarrow x=\left(3,25\right):\left(0,15\right)\cdot\left(-1,2\right)=-26\\ b,\Rightarrow\left|3-2x\right|=4\Rightarrow\left[{}\begin{matrix}3-2x=4\\2x-3=4\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=\dfrac{7}{2}\end{matrix}\right.\)
\(c,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{4}=\dfrac{x+3y-2z}{3+15-8}=\dfrac{20}{10}=2\\ \Rightarrow\left\{{}\begin{matrix}x=6\\y=10\\z=8\end{matrix}\right.\)
\(d,\dfrac{x}{y}=\dfrac{5}{2}\Rightarrow\dfrac{x}{5}=\dfrac{y}{2};\dfrac{y}{z}=\dfrac{1}{3}\Rightarrow\dfrac{y}{1}=\dfrac{z}{3}\Rightarrow\dfrac{y}{2}=\dfrac{z}{6}\\ \Rightarrow\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{z}{6}\)
Đặt \(\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{z}{6}=k\Rightarrow x=5k;y=2k;z=6k\)
\(x^2-y^2+2z^2=372\\ \Rightarrow25k^2-4k^2+72k^2=372\\ \Rightarrow93k^2=372\Rightarrow k^2=4\\ \Rightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=10;y=4;z=12\\x=-10;y=-4;z=-12\end{matrix}\right.\)

Bài 3:
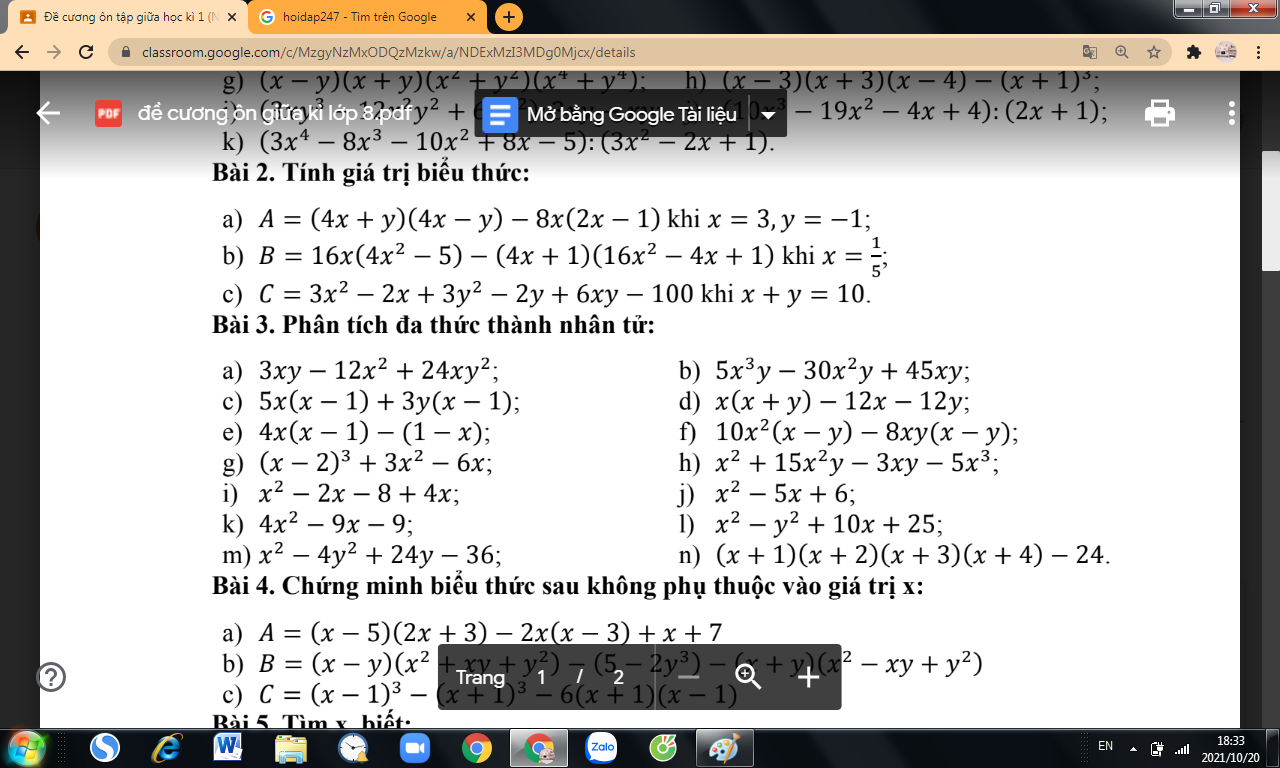
\(a,=3x\left(y-4x+6y^2\right)\\ b,=5xy\left(x^2-6x+9\right)=5xy\left(x-3\right)^2\\ d,=\left(x+y\right)\left(x-12\right)\\ f,=2x\left(x-y\right)\left(5x-4y\right)\\ g,=\left(x-2\right)\left(x-2+3x\right)=\left(x-2\right)\left(4x-2\right)=2\left(x-2\right)\left(2x-1\right)\\ h,=x^2\left(1-5x\right)+3xy\left(5x-1\right)=x\left(1-5x\right)\left(x-3y\right)\\ i,=x\left(x-2\right)+4\left(x-2\right)=\left(x+4\right)\left(x-2\right)\\ j,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ k,=4x^2-12x+3x-9=\left(x-3\right)\left(4x+3\right)\\ l,=\left(x+5\right)^2-y^2=\left(x-y+5\right)\left(x+y+5\right)\\ m,=x^2-\left(2y-6\right)^2=\left(x-2y+6\right)\left(x+2y-6\right)\\ n,=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\\ =\left(x^2+5x+5\right)^2-1-24\\ =\left(x^2+5x+5\right)^2-25\\ =\left(x^2+5x\right)\left(x^2+5x+10\right)\\ =x\left(x+5\right)\left(x^2+5x+10\right)\)

Gọi chiều dài là a(m)
=> Chiều dài là \(\dfrac{5400}{a}\left(m\right)\)
Theo đề bài ta có: \(\dfrac{5400}{a}:a=\dfrac{3}{2}\)
\(\Rightarrow\dfrac{5400}{a^2}=\dfrac{3}{2}\)
\(\Rightarrow a^2=3600\Rightarrow a=60\left(m\right)\)
Vậy chiều rộng là 60m, chiều dài là \(\dfrac{5400}{a}=\dfrac{5400}{60}=90\left(m\right)\)
Chu vi hình chữ nhật là: \(\left(90+60\right).2=300\left(m\right)\)


a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB
c: \(5x\left(x-1\right)+3y\left(x-1\right)=\left(x-1\right)\left(5x+3y\right)\)
e: \(4x\left(x-1\right)-\left(1-x\right)=\left(x-1\right)\left(4x+1\right)\)
j: \(x^2-5x+6=\left(x-2\right)\left(x-3\right)\)