chỉ cần làm bài 4 hộ mình thôi nhế ko cần làm mấy phần kia
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(M=1+2+2^2+...+2^{100}\\ \Rightarrow2M=2+2^2+2^3+...+2^{101}\\ \Rightarrow2M-M=M=2^{101}-1\)
Thế kỉ XXI có 100 năm thì có 25 năm nhuận
Thể tích hình lập phương là \(70\cdot70\cdot70=343000\left(cm^3\right)=343000\left(ml\right)=343\left(l\right)\)
Vậy rót được \(343:6,45=53\left(can\right)\) và dư \(1,15\left(l\right)\)
M=20+21+22+...+2100
2M=21+22+23+...+2101
\(\Rightarrow M=2M-M\)=2101-1
Những năm nhuận ta thấy những năm này chia hết cho 4
Ta thấy trong thế kỉ XXI thì năm nhuận đầu tiên là năm 2004, năm nhuận cuối là năm 2100
Số năm nhuận là (2100-2004):4+1=25 năm
Thể tích thùng hình lập phương là:
70 × 70 × 70 = 343000 (ml) = 343 (lít)
Số ca chứa được nhiều nhất là:
343 : 6,45 = 53 (ca)
Số lít dư còn lại là:
343 - 6,45 × 53 = 1,1t (lít)
Đáp số : 53 ca và dư 1,15 lít.

Trong 1 giờ, kim phút quay được 1 vòng quay; kim giờ quay được \(\dfrac{1}{12}\) vòng quay
Hiệu vận tốc kim phút và kim giờ là: \(1-\dfrac{1}{12}=\dfrac{11}{12}\left(vòng.quay/giờ\right)\)
Lúc 12 giờ, kim phút và kim giờ trùng nhau
Kim giờ và kim phút vuông góc với nhau lần thứ nhât \(\Rightarrow\) kim phút quay nhanh hơn kim giờ là \(\dfrac{3}{12}=\dfrac{1}{4}\left(vòng.quay\right)\)
Khi đó cần ít nhất \(\dfrac{1}{4}:\dfrac{11}{12}=\dfrac{3}{11}\left(giờ\right)\)


Lời giải:
Lời giải:
$372802=300000+70000+2000+800+2$
$430279=400000+30000+200+70+9$
$920300=900000+20000+300$
$704753=700000+4000+700+50+3$

\(P=A.B=\dfrac{\sqrt{x}-1}{\sqrt{x}-3}.\dfrac{\sqrt{x}+6}{\sqrt{x}-1}=\dfrac{\sqrt{x}+6}{\sqrt{x}-3}\)
\(=1+\dfrac{9}{\sqrt{x}-3}\le1+\dfrac{9}{0-3}=1-3=-2\)
\(maxP=-2\Leftrightarrow x=0\)
\(1,x=16\Leftrightarrow A=\dfrac{4-1}{4-3}=\dfrac{3}{1}=3\\ 2,B=\dfrac{x+2\sqrt{x}-3+5\sqrt{x}+5+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x+7\sqrt{x}+6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ B=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+6\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}+6}{\sqrt{x}-1}\\ 3,P=AB=\dfrac{\sqrt{x}-1}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}+6}{\sqrt{x}-1}=\dfrac{\sqrt{x}+6}{\sqrt{x}-3}\\ P=1+\dfrac{9}{\sqrt{x}-3}\\ Vì.\sqrt{x}-3\ge-3\Leftrightarrow\dfrac{9}{\sqrt{x}-3}\le-3\\ \Leftrightarrow P=1+\dfrac{9}{\sqrt{x}-3}\le1-3=-2\\ P_{max}=-2\Leftrightarrow x=0\)

a/
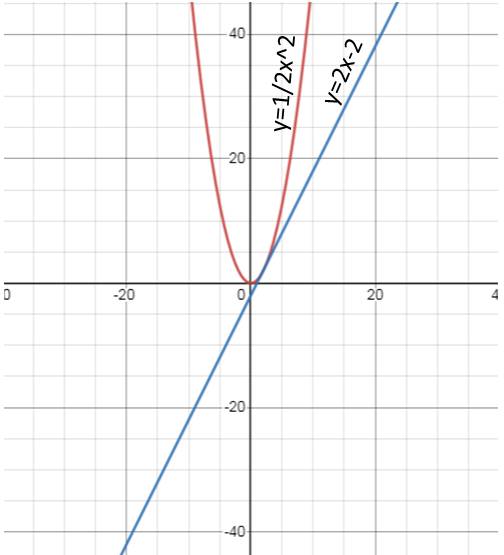
b/
Tọa độ giao điểm của 2 đồ thị là:
\(\dfrac{1}{2}x^2=2x-2\\ \Leftrightarrow\dfrac{1}{2}x^2-2x+2=0\\ \Leftrightarrow x=2\)
b) Phương trình hoành độ giao điểm của (P) và (d):
1/2 x² = 2x - 2
⇔x² = 4x - 4
⇔x² - 4x + 4 = 0
⇔(x - 2)² = 0
⇔x - 2 = 0
⇔x = 2
⇔y = 2.2 - 2 = 2
Vậy tọa độ giao điểm của (P) và (d) là (2;2)
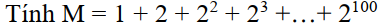


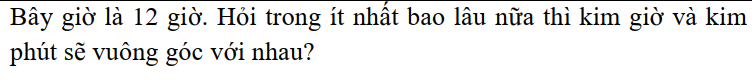


 Làm hộ mình câu 5 thôi nhé !
Làm hộ mình câu 5 thôi nhé !
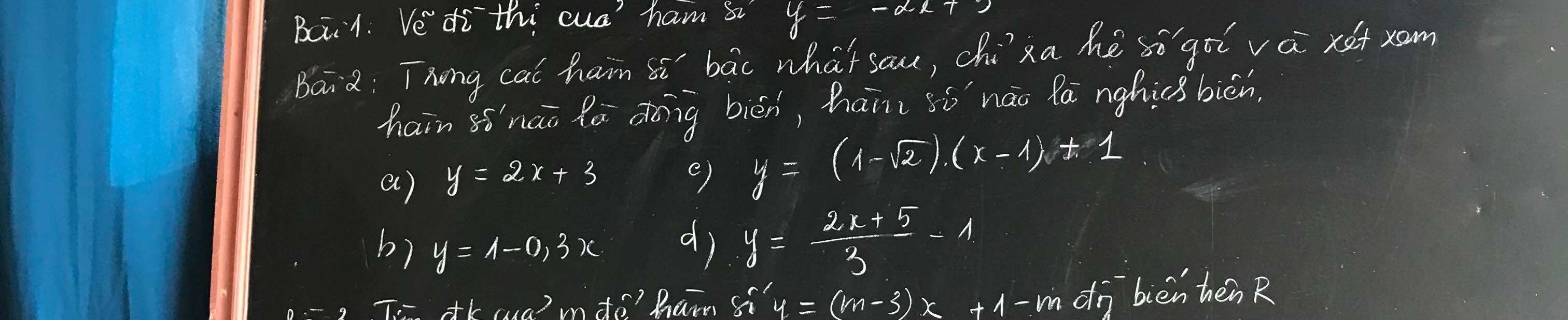






 giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
ko biết
\(\tan a=\frac{22,1}{S}\)
\(\cot a=\frac{s}{22,1}\)
b , Khi \(a=1^015'=\frac{22,1}{s}\Rightarrow S=\frac{22,1}{\tan1^015'}=1012,83\left(m\right)\)