Tìm x : ( x - 1 ) ^2 = ( x - 1 )^4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 2 2021
Bạn vào biểu tượng \(\Sigma\) để nhập biểu thức cho chính xác nhé
18 tháng 8 2021
Bài 1:
Ta có: \(4-2\left(x+1\right)=2\)
\(\Leftrightarrow2\left(x+1\right)=2\)
\(\Leftrightarrow x+1=1\)
hay x=0
Bài 2:
Ta có: \(\left|2x-3\right|-1=2\)
\(\Leftrightarrow\left|2x-3\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3\\2x-3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=0\end{matrix}\right.\)
NL
3
25 tháng 12 2022
\(3\left(x-2\right)+4\left(x-1\right)=25\)
\(\Leftrightarrow3x-6+4x-4=25\)
\(\Leftrightarrow7x=35\)
\(\Leftrightarrow x=5\)
25 tháng 12 2022
\(\left(5x-3\right)\left(x-2\right)=\left(x-1\right)\left(x-2\right)\)
\(\Leftrightarrow\left(5x-3\right)\left(x-2\right)-\left(x-1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(5x-3-x+1\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(4x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\4x+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{-1}{2}\end{matrix}\right.\)
NT
0
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
1.
$x(x+2)(x+4)(x+6)+8$
$=x(x+6)(x+2)(x+4)+8=(x^2+6x)(x^2+6x+8)+8$
$=a(a+8)+8$ (đặt $x^2+6x=a$)
$=a^2+8a+8=(a+4)^2-8=(x^2+6x+4)^2-8\geq -8$
Vậy $A_{\min}=-8$ khi $x^2+6x+4=0\Leftrightarrow x=-3\pm \sqrt{5}$
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
2.
$B=5+(1-x)(x+2)(x+3)(x+6)=5-(x-1)(x+6)(x+2)(x+3)$
$=5-(x^2+5x-6)(x^2+5x+6)$
$=5-[(x^2+5x)^2-6^2]$
$=41-(x^2+5x)^2\leq 41$
Vậy $B_{\max}=41$. Giá trị này đạt tại $x^2+5x=0\Leftrightarrow x=0$ hoặc $x=-5$
A
2
15 tháng 10 2017
\(8\left(x+\frac{1}{x}\right)^2+4\left(x^2+\frac{1}{x^2}\right)^2-4\left(x^2+\frac{1}{x^2}\right)\left(x+\frac{1}{x}\right)^2=\left(x+4\right)^2\)
ĐKXĐ : \(x\ne0\)
Ta có \(pt\Leftrightarrow8\left(x^2+\frac{1}{x^2}+2\right)+4\left(x^2+\frac{1}{x}\right)^2-4\left(x^2+\frac{1}{x^2}\right)\left(x^2+\frac{1}{x^2}+2\right)=\left(x+4\right)^2\)
Đặt \(x^2+\frac{1}{x^2}=a\) thay vào pt trên ta có :
\(pt\Leftrightarrow8\left(a+2\right)+4a^2-4.a.\left(a+2\right)=\left(x+4\right)^2\)
\(\Leftrightarrow8a+16+4a^2-4a^2-8a=\left(x+4\right)^2\)
\(\Leftrightarrow\left(x+4\right)^2=16\Leftrightarrow\orbr{\begin{cases}x+4=4\\x+4=-4\end{cases}\Rightarrow\orbr{\begin{cases}x=0\left(KTMĐKXĐ\right)\\x=-8\left(TMĐKXĐ\right)\end{cases}}}\)
Vậy \(x=-8\)
\(\)
18 tháng 2 2021
a) Ta có: \(P=\left(\dfrac{x^2-1}{x^4-x^2+1}+\dfrac{2}{x^6+1}-\dfrac{1}{x^2+1}\right)\cdot\left(x^2-\dfrac{x^4+x^2-1}{x^4+x^2+1}\right)\)
\(=\left(\dfrac{\left(x^2-1\right)\left(x^2+1\right)}{\left(x^2+1\right)\left(x^4-x^2+1\right)}+\dfrac{2}{\left(x^2+1\right)\left(x^4-x^2+1\right)}-\dfrac{x^4-x^2+1}{\left(x^2+1\right)\left(x^4-x^2+1\right)}\right)\cdot\left(\dfrac{x^2\left(x^4+x^2+1\right)}{x^4+x^2+1}-\dfrac{x^4+x^2-1}{x^4+x^2+1}\right)\)
\(=\dfrac{x^4-1+2-x^4+x^2-1}{\left(x^2+1\right)\cdot\left(x^4-x^2+1\right)}\cdot\dfrac{x^6+x^4+x^2-x^4-x^2+1}{x^4+x^2+1}\)
\(=\dfrac{x^2}{\left(x^2+1\right)\left(x^4-x^2+1\right)}\cdot\dfrac{x^6+1}{x^4+x^2+1}\)
\(=\dfrac{x^2}{\left(x^2+1\right)\left(x^4-x^2+1\right)}\cdot\dfrac{\left(x^2+1\right)\left(x^4-x^2+1\right)}{x^4+x^2+1}\)
\(=\dfrac{x^2}{x^4+x^2+1}\)
A
0
21 tháng 6 2021
a) (2x + 1)(1 - 2x) + (1 - 2x)2 = 18
= ( 1 - 2x) \(\left[\left(2x+1+1-2x\right)\right]\) = 18
= 2(1 - 2x) - 18 = 0
= 2 - 4x - 18 = 0
= -16 - 4x = 0
= -4x = 16
= x = \(\dfrac{16}{-4}=-4\)
b) 2(x + 1)2 -(x - 3)(x + 3) - (x - 4)2 = 0
= 2 (x2 + 2x + 1) - (x2 - 9) - (x2 - 8x + 16) = 0
= 2x2 + 4x + 2 - x2 + 9 - x2 + 8x - 16 = 0
= 12x - 5 = 0
= 12x = 5
= x = \(\dfrac{5}{12}\)
c) (x - 5)2 - x(x - 4) = 9
= x2 - 10x + 25 - x2 + 4x - 9 = 0
= -6x + 16 = 0
= -6x = -16
= x = \(\dfrac{-16}{-6}=\dfrac{8}{3}\)
d) (x - 5)2 + (x - 4)(1 - x)
= x2 - 10x + 25 + 5x - x2 - 4 = 0
= -5x + 21 = 0
= -5x = -21
= x = \(\dfrac{-21}{-5}=\dfrac{21}{5}\)
Chúc bạn học tốt
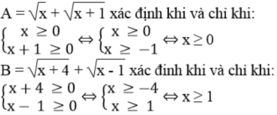
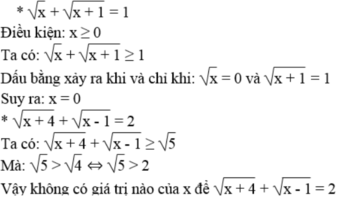
x=1 hoặc 0
\(\left(x-1\right)^2=\left(x-1\right)^4\)
\(\Rightarrow\left(x-1\right)^2-\left(x-1\right)^4=0\)
\(\Rightarrow\left(x-1\right)^2\left[1-\left(x-1^2\right)\right]=0\)
\(\Rightarrow\orbr{\begin{cases}\left(x-1\right)^2=0\\1-\left(x-1\right)^2=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x-1=0\\\left(x-1\right)^2=1\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=1\\x-1=\pm1\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=1\\x=2;x=0\end{cases}}\)
_Học tốt_