Giải phương trình : 4x4+7x2-2=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
14 tháng 9 2019
4x4 + x2 – 5 = 0;
Đặt x2 = t (t ≥ 0). Phương trình trở thành:
4t2 + t - 5 = 0
Nhận thấy phương trình có dạng a + b + c = 0 nên phương trình có nghiệm
t1 = 1; t2 =(-5)/4
Do t ≥ 0 nên t = 1 thỏa mãn điều kiện
Với t = 1, ta có: x2 = 1 ⇔ x = ±1
Vậy phương trình có 2 nghiệm x1 = 1; x2 = -1
CM
22 tháng 12 2017
2x4 – 7x2 + 5 = 0 (1)
Tập xác định: D = R.
Đặt t = x2, điều kiện t ≥ 0.
Khi đó phương trình (1) trở thành:
2t2 – 7t + 5 = 0
⇔ (2t – 5) (t – 1) = 0
PT
1
CM
18 tháng 4 2019
a) 4 x 4 + x 2 − 5 = 0
Đặt x 2 = t (t ≥ 0). Phương trình trở thành:
4 t 2 + t − 5 = 0
Nhận thấy phương trình có dạng a + b + c = 0 nên phương trình có nghiệm
t 1 = 1 ; t 2 = ( − 5 ) / 4
Do t ≥ 0 nên t = 1 thỏa mãn điều kiện
Với t = 1, ta có: x 2 = 1 ⇔ x = ± 1
Vậy phương trình có 2 nghiệm x 1 = 1 ; x 2 = − 1
b) 3 x 4 + 4 x 2 + 1 = 0
Đặt x 2 = t ( t ≥ 0 ) . Phương trình trở thành:
3 t 2 + 4 t + 1 = 0
Nhận thấy phương trình có dạng a - b + c = 0 nên phương trình có nghiệm
t 1 = - 1 ; t 2 = ( - 1 ) / 3
Cả 2 nghiệm của phương trình đều không thỏa mãn điều kiện t ≥ 0
Vậy phương trình đã cho vô nghiệm.
CM
10 tháng 9 2018
7x2 - 6√2x + 2 = 0
a = 7; b' = -3√2; c = 2
Δ' =(b')2 - ac = (-3√2)2 - 7.2 = 4 ⇒ √(Δ') = 2
Phương trình có 2 nghiệm:
x1 = (3√2 + 2)/7; x2 = (3√2 - 2)/7
CM
13 tháng 2 2017
a) 3 x 2 + 8 x + 4 = 0 ;
a = 3; b' = 4; c = 4
Δ ' = ( b ' ) 2 - a c = 4 2 - 3 . 4 = 4 ⇒ √ ( Δ ' ) = 2
Phương trình có 2 nghiệm:
x 1 = ( - 4 + 2 ) / 3 = ( - 2 ) / 3 ; x 2 = ( - 4 - 2 ) / 3 = - 2
b) 7 x 2 - 6 √ 2 x + 2 = 0
a = 7; b' = -3√2; c = 2
Δ ' = ( b ' ) 2 - a c = ( - 3 √ 2 ) 2 - 7 . 2 = 4 ⇒ √ ( Δ ' ) = 2
Phương trình có 2 nghiệm:
x 1 = ( 3 √ 2 + 2 ) / 7 ; x 2 = ( 3 √ 2 - 2 ) / 7
CM
13 tháng 9 2019
Phương trình bậc hai: 7x2 – 2x + 3 = 0
Có: a = 7; b = -2; c = 3; Δ = b2 – 4ac = (-2)2 – 4.7.3 = -80 < 0
Vậy phương trình vô nghiệm.
CM
9 tháng 2 2019
a) Phương trình bậc hai: 7 x 2 – 2 x + 3 = 0
Có: a = 7; b = -2; c = 3; Δ = b 2 – 4 a c = ( - 2 ) 2 – 4 . 7 . 3 = - 80 < 0
Vậy phương trình vô nghiệm.
b) Phương trình bậc hai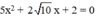 
Có: a = 5; b = 2√10; c = 2; Δ = b 2 – 4 a c = ( 2 √ 10 ) 2 – 4 . 2 . 5 = 0
Vậy phương trình có nghiệm kép.
c) Phương trình bậc hai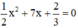 
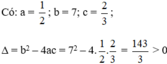
Vậy phương trình có hai nghiệm phân biệt.
d) Phương trình bậc hai 1 , 7 x 2 – 1 , 2 x – 2 , 1 = 0
Có: a = 1,7; b = -1,2; c = -2,1;
Δ = b 2 – 4 a c = ( - 1 , 2 ) 2 – 4 . 1 , 7 . ( - 2 , 1 ) = 15 , 72 > 0
Vậy phương trình có hai nghiệm phân biệt.
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt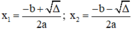 
+ Nếu Δ = 0, phương trình có nghiệm kép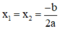 
;
+ Nếu Δ < 0, phương trình vô nghiệm.
CM
6 tháng 11 2017
Ta có: a = 7, b= 2(m-1), c = - m2
Suy ra: Δ' = (m - 1)2 + 7m2
Do (m-1)2 ≥ 0 mọi m và m2 ≥ 0 mọi m
=> ∆’≥ 0 với mọi giá trị của m.
Do đó phương trình có nghiệm với mọi giá trị của m.
Đặt \(k=x^2\left(k\ge0\right)\)
Phương trình trở thành \(4k^2+7k-2=0\)
Ta có: \(\Delta=7^2+4.4.2=81,\sqrt{\Delta}=9\)
\(\Rightarrow\orbr{\begin{cases}k=\frac{-7+9}{8}=\frac{1}{4}\\k=\frac{-7-9}{8}=-2\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x^2=\frac{1}{4}\\x^2=-2\left(VL\right)\end{cases}}\)
Vậy phương trình có 2 nghiệm \(\left\{\pm\frac{1}{2}\right\}\)
\(x=\pm\frac{1}{2}\)