Giải bài toán sau bằng cách lập hệ phương trình: Hai đội công nhân I và II được giao sửa một đoạn đường. Nếu cả hai đội cùng làm chung thì sau 4 giờ là hoàn thành công việc. Nếu đội I làm một mình trong 2 giờ, sau đó đội II tiếp tục làm một mình trong 3 giờ thì họ đã hoàn thành được 7 12 công việc. Hỏi mỗi đội làm riêng thì sẽ hoàn thành công việc trong bao lâu.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi thời gian đội I, đội II làm một mình xong công việc lần lượt là x, y (đơn vị ngày, đk :x, y > 4)
+ Thì mỗi ngày đội I làm được 1/x (công việc), đội II được 1/y (công việc)
Vì hai đội cùng làm thì 4 ngày xong nên mỗi ngày hai đội làm được 1/4 (công việc), nên ta có phương trình 1/x + 1/y =1/4.
+ Phần công việc đội I làm trong 3 ngày là 3/x (công việc), phần công việc đội II làm trong 6 ngày là 6/y. Vì khi đội I làm 3 ngày, đội II làm 6 ngày thì xong công việc nên ta có pt : 3/x + 6/y = 1
ta có hpt :1/x + 1/y =1/4 và 3/x + 6/y = 1
=> x=6 , y=12
k mk nha!!

Gọi vận tốc của đội 1 và 2 trong 1 ngày lần lượt là x,y(x,y>0)
theo đề bài ,ta có
15(x+y)=1 hay 15x+15y=1 hay \(x=\frac{1-15y}{15}\)(1)
và 5(x+y)+24x=1 hay 29x+5y =1(**)
Thay (1)vào (**), ta có
\(29\frac{1-15y}{15}+5y=1\Rightarrow y=\frac{7}{180}\Rightarrow x=\frac{1}{36}\)
Vậy đội 1 làm trong 36 ngày
đội 2 làm trong180/7 ngày

Gọi số ngày mình đội 1 làm xong công việc là x ngày ( x > 0 )
Ta có:đội 1 làm 9 ngày thì bằng 2 đội làm ( 4-1 ) bằng 3 ngày
=> Đội 1 làm 6 ngày thì bằng 2 đội làm trong 3 ngày
=> Mình đội 2 làm xong công việc là \(\frac{x}{2}\)(ngày)
1 ngày đội 1 làm được là:\(\frac{1}{x}\)( phần công việc)
1 ngày đội 2 làm được là:\(1:\frac{x}{2}=\frac{2}{x}\)(phần công việc)
Theo bài ra ta có PT:\(\frac{1}{x}+\frac{2}{x}=\frac{1}{4}\)
\(\Rightarrow x=12\left(TM\right)\)
Vậy đội 1 làm một mình hết 12 ngày
đội 2 làm một mình hết \(\frac{12}{2}=6\) ngày

Gọi x (giờ) là thời gian đội I làm một mình xong công việc (x > 12)
Thời gian đội thứ II làm một mình xong công việc là: x – 7 (giờ)
Trong một giờ đội I làm được 1/x (công việc)
Trong một giờ đội II làm được 1/(x-7) (công việc)
Trong một giờ cả hai đội làm được 1/12 (công việc)
Theo bài ra ta có phương trình:
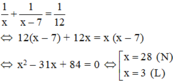
Vậy thời gian đội I làm xong công việc là 28 giờ, thời gian đội II làm xong công việc là: 28 – 7 = 21 (giờ)
Đáp án: C

gọi thời gian đội1;đội 2 làm riêng hoàn thành công việc lần lượt là x;y(h)
đk: x;y>0
năng suất làm riêng của đội 1 là: 1/x (công việc/h)
năng suất làm riêng của đội 2 là: 1/y (công việc/h)
năng suất làm chung của cả 2 đội là: \(\frac{1}{x}+\frac{1}{y}=\frac{x+y}{xy}\)(công việc/h)
thời gian 2 đội làm chung hoàn thành công việc là:\(\frac{xy}{x+y}\left(h\right)\)
vì nếu 2 đội làm chung thì sau 4h hoàn thành nên ta có phương trình:
\(\frac{xy}{x+y}=4\Leftrightarrow4x+4y=xy\)(1)
khối lượng công việc đội 1 làm riêng được trong 2h là: 2/x (công việc)
khối lượng công việc đội 2 làm riêng được trong 3h là: 3/y(công việc)
vì nếu đội1 ; đội 2 lần lượt làm riêng trong 2h; 3h thì hoàn thành được 7/12 công việc nên ta có phương trình:
\(\frac{2}{x}+\frac{3}{y}=\frac{7}{12}\) \(\Leftrightarrow36x+24y=7xy\)(2)
từ (1) và (2) ta có hệ phương trình:\(\left\{{}\begin{matrix}4x+4y=xy\\36x+24y=7xy\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=12\end{matrix}\right.\)(tm)
vậy thời gian đội1;đội 2 làm riêng hoàn thành công việc lần lượt là 6h;12h