Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (giờ) là thời gian đội I làm một mình xong công việc (x > 12)
Thời gian đội thứ II làm một mình xong công việc là: x – 7 (giờ)
Trong một giờ đội I làm được 1/x (công việc)
Trong một giờ đội II làm được 1/(x-7) (công việc)
Trong một giờ cả hai đội làm được 1/12 (công việc)
Theo bài ra ta có phương trình:
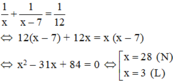
Vậy thời gian đội I làm xong công việc là 28 giờ, thời gian đội II làm xong công việc là: 28 – 7 = 21 (giờ)
Đáp án: C

Gọi a(giờ) là thời gian đội 1 hoàn thành công việc khi làm riêng
Gọi b(giờ) là thời gian đội 2 hoàn thành công việc khi làm riêng
(Điều kiện: a>0; b>0)
Trong 1 giờ, đội 1 làm được: \(\dfrac{1}{a}\)(công việc)
Trong 1 giờ, đội 2 làm được: \(\dfrac{1}{b}\)(công việc)
Trong 1 giờ, hai đội làm được: \(\dfrac{1}{4}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{4}\)(1)
Vì khi đội 1 làm trong 2 giờ, sau đó đội 2 làm một mình trong 3 giờ thì họ hoàn thành được \(\dfrac{7}{12}\) công việc nên ta có phương trình:
\(\dfrac{2}{a}+\dfrac{3}{b}=\dfrac{7}{12}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{4}\\\dfrac{2}{a}+\dfrac{3}{b}=\dfrac{7}{12}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{a}+\dfrac{2}{b}=\dfrac{1}{2}\\\dfrac{2}{a}+\dfrac{3}{b}=\dfrac{7}{12}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-1}{b}=-\dfrac{1}{12}\\\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=12\\\dfrac{1}{a}=\dfrac{1}{4}-\dfrac{1}{12}=\dfrac{1}{6}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=6\\b=12\end{matrix}\right.\)(thỏa ĐK)
Vậy: Đội 1 cần 6 giờ để hoàn thành công việc khi làm một mình
Đội 2 cần 12 giờ để hoàn thành công việc khi làm một mình

Gọi thời gian làm riêng để hoàn thành công việc của đội 1 là x>0 (ngày), đội 2 là y>0 (ngày)
Trong 1 ngày hai đội lần lượt làm được \(\dfrac{1}{x}\) và \(\dfrac{1}{y}\) phần công việc
Do 2 đội làm chung thì hoàn thành sau 12 ngày nên: \(12\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\)
Do đội 1 hoàn thành chậm hơn đội 2 là 10 ngày nên: \(x=y+10\)
Ta có hệ pt:
\(\left\{{}\begin{matrix}12\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\\x=y+10\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}12\left(\dfrac{1}{y+10}+\dfrac{1}{y}\right)=1\\x=y+10\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}12\left(2y+10\right)=y\left(y+10\right)\\x=y+10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y^2-14y-120=0\\x=y+10\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y=20\\x=30\end{matrix}\right.\)

Gọi thời gian mà đội 1 làm một mình xong cv là x (ngày) x > 0
Gọi thời gian mà đội 2 làm một mình xong cv là y (ngày) y > 0
Một ngày cả hai đội làm được 1/x + 1/y = 1/12 cv (1)
Nếu làm riêng 1 mình đội 1 nhanh hơn đội 2 là 7 ngày nên: x + 7 = y (2)
Giải hệ 2 pt trên ta được x = 21, y = 28

Gọi thời gian đội 1 và đội 2 hoàn thành công việc một mình lần lượt là x(ngày), y( ngày)(x,y>12)
Mỗi ngày đội 1 làm được phẫn việc là 1/x
Đội 2 làm được số phần việc là 1/y
cả hai đội làm được số phần việc là 1/12
ta có phương trình: 1/x+1/y=1/12(1)
Đội 1 làm trong 5 ngày rồi nghỉ, dội 2 làm tiếp 15 ngày thì họ làm được 75%công việc
từ đó ta có phương trình: 5/x+15/y=3/4(2)
Từ (1)(2) ta có hệ phương trình:{1/x+1/y=1/12; 5/x+15/y=3/4
Giải hệ pt ta tìm được x=20; y=30
KL:Nếu làm một mình thì đội thứ nhất hoàn thành công việc trong 20 ngày, đội thứ hai hoàn thành công việc trong 30 ngày.

Gọi x ( giờ ) là thời gian đội 1 làm một mình xong công việc ( x > 12 )
Thời gian đội thứ 2 làm một mình xong công việc là : \(x-7\left(giờ\right)\)
Trong một giờ đội 1 làm được \(\dfrac{1}{x}\left(\text{công việc}\right)\)
Trong một giờ đội 2 làm được \(\dfrac{1}{x-7}\left(\text{công việc}\right)\)
Trong một giờ cả hai đội làm được \(\dfrac{1}{12}\left(\text{công việc}\right)\)
Theo bài ra ta có pt : \(\dfrac{1}{x}+\dfrac{1}{x-7}=\dfrac{1}{12}\Leftrightarrow12\left(x-7\right)+12x=x\left(x-7\right)\Leftrightarrow x^2-31x+84=0\Leftrightarrow\left\{{}\begin{matrix}x=28\left(N\right)\\x=3\left(L\right)\end{matrix}\right.\)
Vậy thời gian đội 1 làm xong công việc là 8 giờ , thời gian đội 2 làm xong công việc là : \(28-7=21\left(giờ\right)\)
gọi thời gian đội1;đội 2 làm riêng hoàn thành công việc lần lượt là x;y(h)
đk: x;y>0
năng suất làm riêng của đội 1 là: 1/x (công việc/h)
năng suất làm riêng của đội 2 là: 1/y (công việc/h)
năng suất làm chung của cả 2 đội là: \(\frac{1}{x}+\frac{1}{y}=\frac{x+y}{xy}\)(công việc/h)
thời gian 2 đội làm chung hoàn thành công việc là:\(\frac{xy}{x+y}\left(h\right)\)
vì nếu 2 đội làm chung thì sau 4h hoàn thành nên ta có phương trình:
\(\frac{xy}{x+y}=4\Leftrightarrow4x+4y=xy\)(1)
khối lượng công việc đội 1 làm riêng được trong 2h là: 2/x (công việc)
khối lượng công việc đội 2 làm riêng được trong 3h là: 3/y(công việc)
vì nếu đội1 ; đội 2 lần lượt làm riêng trong 2h; 3h thì hoàn thành được 7/12 công việc nên ta có phương trình:
\(\frac{2}{x}+\frac{3}{y}=\frac{7}{12}\) \(\Leftrightarrow36x+24y=7xy\)(2)
từ (1) và (2) ta có hệ phương trình:\(\left\{{}\begin{matrix}4x+4y=xy\\36x+24y=7xy\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=12\end{matrix}\right.\)(tm)
vậy thời gian đội1;đội 2 làm riêng hoàn thành công việc lần lượt là 6h;12h