Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: BC=13cm
\(AB=3\sqrt{13}\left(cm\right)\)
\(AC=2\sqrt{13}\left(cm\right)\)
cho tam giác ABC và 3 điểm A',B',C' lần lượt nằm trên 3 cạnh BC,AC,AB ( A',B',C' không trùng với các đỉnh của tam giác )
Khi đó ta có : AA',BB',CC' đồng quy \(\Leftrightarrow\frac{A'B}{A'C}.\frac{B'C}{B'A}.\frac{C'A}{C'B}=1\)
Gọi P là giao điểm của AD và BE
Áp dụng định lí Ceva vào \(\Delta ABE\),ta có :
\(\frac{BP}{PE}.\frac{HE}{AH}.\frac{AM}{BM}=1\Rightarrow\frac{AH}{HE}=\frac{BP}{PE}\Rightarrow PH//AB\)
\(\Rightarrow\widehat{BAD}=\widehat{DPH}\)
Mà \(\widehat{BAD}=\widehat{DAH}\)
\(\Rightarrow\widehat{DAH}=\widehat{PDH}\Rightarrow\Delta AHP\)cân tại H
\(\Rightarrow HP=AH\)
Cần chứng minh \(DP//CE\Leftrightarrow\frac{BD}{BC}=\frac{BP}{BE}\Leftrightarrow\frac{BD}{BC}=1-\frac{EP}{BE}\)
Ta có : \(\frac{EP}{BE}=\frac{HP}{AB}=\frac{AH}{AB}=\frac{HD}{BD}\)
Khi đó : \(\frac{BD}{BC}=1-\frac{HD}{BD}\Leftrightarrow\frac{BD}{BC}+\frac{HD}{BD}=1\Leftrightarrow BD^2+HD.BC=BC.BD=\left(BD+DC\right).BD\)
\(\Rightarrow HD.BC=CD.BD\Rightarrow\frac{HD}{BD}=\frac{CD}{BC}\Leftrightarrow\frac{AH}{AB}=\frac{CD}{BC}\)
Ta có : \(\widehat{CDA}=\widehat{DBA}+\widehat{BAD}=\widehat{CAH}+\widehat{DAH}=\widehat{CAD}\)
\(\Rightarrow\Delta CAD\)cân tại C \(\Rightarrow CD=CA\)
Từ đó suy ra : \(\frac{AH}{AB}=\frac{AC}{BC}\) ( đúng vì \(\Delta AHB~\Delta CAB\left(g.g\right)\))
Vậy ta có đpcm
1 phần thôi nhé
Nối BE, Gọi P là giao điểm của AD với BE.
Áp dụng định lí Ceva cho tam giác ABE => AH/HE=BP/PE=> HP//AB(1).
Từ (1)=> Tam giác AHP cân tại H=> AH=HP.(2)
Ta cần chứng minh AD//CE <=> DP//CE <=> BD/BC=BP/BE <=> BD/BC=1-(EP/BE).(3)
Mà EP/BE=HP/AB (do (1))=> EP/BE= AH/AB=HD/DB (do (2) và tc phân giác). (4)
Khi đó (3)<=> BD/BC=1-(HD/DB) hay (BD/BC)+(HD/DB)=1 <=> BD^2+HD*BC=BC*DB
<=> BD^2+HD*BC= (BD+DC)*BD <=> BD^2+HD*BC= BD^2+BD*DC <=> HD*BC=BD*DC
<=> HD/DB=CD/BC <=> AH/AB=CD/BC. (5)
Chú ý: Ta cm được: CA=CD (biến đổi góc).
Nên (5) <=> AH/AB=CA/BC <=> Tg AHB đồng dạng Tg CAB.( luôn đúng)
=> DpCm.
a: Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC và AC^2=CH*BC
=>AB^2/AC^2=BH/CH
b: S AHC=8,64
=>1/2*AH*HC=8,64
=>AH*HC=17,28
S AHB=15,36
=>1/2*AH*HB=15,36
=>AH*HB=30,72
mà AH*HC=17,28
nên AH*AH*HB*HC=30,72*17,28
=>AH^2*AH^2=30,72*17,28
=>AH^4=530,8416
=>\(AH=\sqrt[4]{530.8416}=4.8\left(cm\right)\)
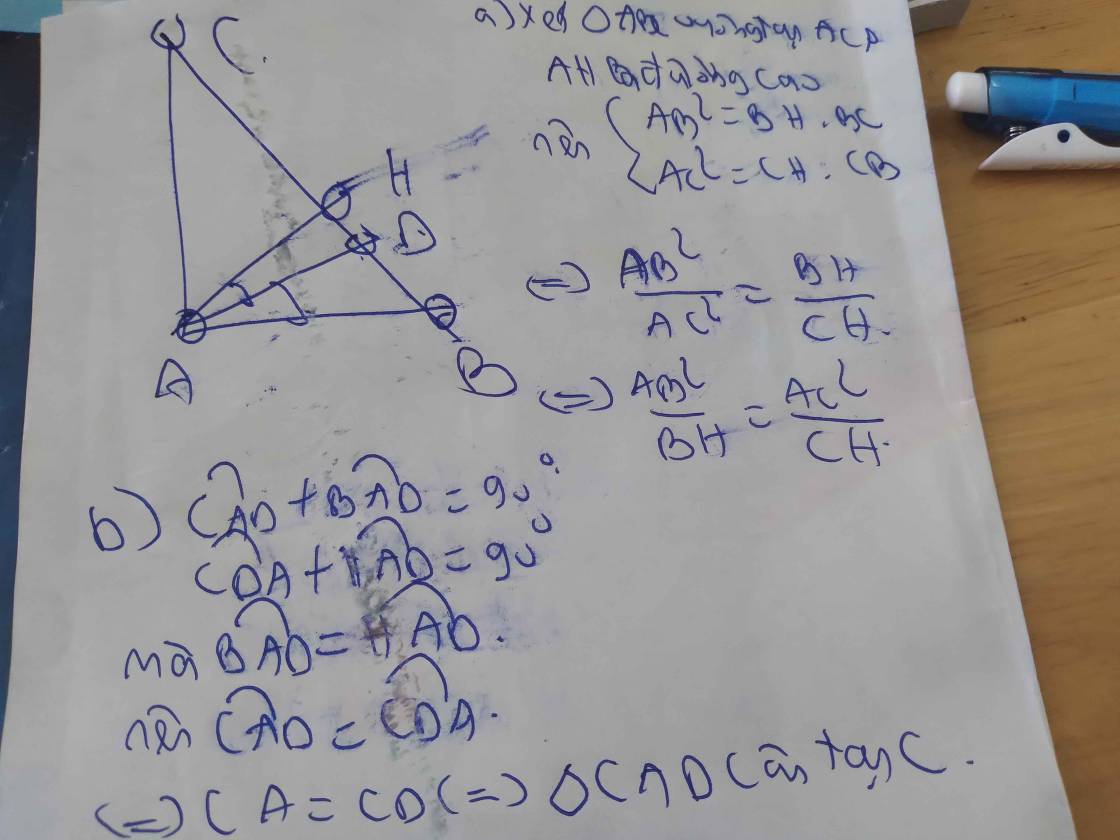
\(\Delta AHC\sim\Delta BHA\Rightarrow\frac{AB}{AC}=\frac{AH}{CH}=\frac{BH}{AH}\Rightarrow\left\{{}\begin{matrix}AH^2=BH.CH\left(1\right)\\\frac{AB^2}{AC^2}=\frac{AH^2}{CH^2}\left(2\right)\end{matrix}\right.\)
Tư f (1) \(\Rightarrow\frac{AH^2}{CH}=BH\Rightarrow\frac{AH^2}{CH^2}=\frac{BH}{CH}\left(3\right)\)
Từ 2 và 3 suy ra ĐPCM
câu c cơ