Chứng minh rằng phương trình \(4x^5+2018x+2019=0\) có duy nhất một nghiệm thực.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KH
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
Để chứng minh pt có đúng 1 nghiệm thì phải sử dụng kiến thức đơn điệu của lớp 12: hàm đơn điệu trên 1 khoảng thì có tối đa 1 nghiệm trên khoảng ấy
Đặt \(f\left(x\right)=4x^5+20188x+2019\)
\(f\left(x\right)\) là hàm đa thức nên liên tục trên R
\(f\left(0\right)=2019>0\)
\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=\lim\limits_{x\rightarrow-\infty}x^5\left(4+\dfrac{20188}{x^4}+\dfrac{2019}{x^5}\right)=-\infty.4=-\infty< 0\)
\(\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm trên \(\left(-\infty;0\right)\) (1)
Mặt khác \(f'\left(x\right)=20x^4+20188>0;\forall x\)
\(\Rightarrow f\left(x\right)\) đồng biến trên R
\(\Rightarrow f\left(x\right)\) có tối đa 1 nghiệm trên R (2)
(1);(2) \(\Rightarrow f\left(x\right)\) có đúng 1 nghiệm thực trên R
CM
29 tháng 11 2017
- Xét hàm số f ( x ) = x 3 + x - 1 , ta có f(0) = -1 và f(1) = 1 nên: f(0).f(1) < 0.
- Mặt khác: f ( x ) = x 3 + x - 1 là hàm đa thức nên liên tục trên [0;1].
- Suy ra f ( x ) = x 3 + x - 1 đồng biến trên R nên phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 ∈ ( 0 ; 1 ) .
- Theo bất đẳng thức Côsi:
15 tháng 8 2018
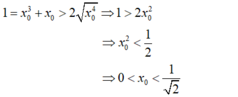
a(x-a)2 + b(x-b)2 = 0
<=> (a + b)x2 - (2a2 + 2b2)x + a3 + b3 = 0
Xét a + b = 0
<=> a = - b thì phương trình trở thành
0 = 0 (đúng)
Xét a \(\ne\)- b
Để có nghiệm duy nhất thì
∆ = (a2 + b2)2 - (a + b)(a3 + b3) = 0
<=> ab(a - b)2 = 0
<=> a = b
Vậy |a| = |b|
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
\(VT=\left|x-1\right|+\left|2-x\right|\ge\left|x-1+2-x\right|=1\)
\(VP=-4x^2+12x-9-1=-\left(2x-3\right)^2-1\le-1\)
\(\Rightarrow VT>VP\) ; \(\forall x\)
\(\Rightarrow\) Pt đã cho luôn luôn vô nghiệm
b.
\(\Leftrightarrow\left(m^2+3m\right)x=-m^2+4m+21\)
\(\Leftrightarrow m\left(m+3\right)x=\left(7-m\right)\left(m+3\right)\)
Để pt có nghiệm duy nhất \(\Rightarrow m\left(m+3\right)\ne0\Rightarrow m\ne\left\{0;-3\right\}\)
Khi đó ta có: \(x=\dfrac{\left(7-m\right)\left(m+3\right)}{m\left(m+3\right)}=\dfrac{7-m}{m}\)
Để nghiệm pt dương
\(\Leftrightarrow\dfrac{7-m}{m}>0\Leftrightarrow0< m< 7\)
MH
Chứng minh rằng tồn tại một cặp số duy nhất (x, y) thỏa mãn phương trình:
\(x^2-4x+y-6\sqrt{y}+13=0\)
3
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 4 2021
Đề bài sai
Chỉ tồn tại duy nhất cặp x;y thỏa mãn pt khi đề bài là:
\(x^2-4x+y-6\sqrt{y}+13=0\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 4 2021
ĐKXĐ: ...
\(\Leftrightarrow\left(x^2-4x+4\right)+\left(y-6\sqrt{y}+9\right)=0\)
\(\Leftrightarrow\left(x-2\right)^2+\left(\sqrt{y}-3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\\sqrt{y}-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=9\end{matrix}\right.\)
Vậy có duy nhất cặp số (x;y)=(2;9) thỏa mãn phương trình
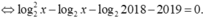
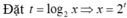
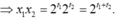
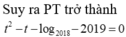
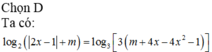
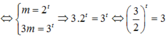
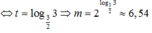
Dùng tính liên tục để chứng minh nó có nghiệm, và dùng đạo hàm chứng minh nghiệm đó là duy nhất.
Được phép sử dụng kiến thức 12 để giải ko bạn? Lớp 10 thì chắc là chịu, tối thiểu cũng phải lớp 11 mới chứng minh được pt này có nghiệm :D