Bài 2: Cho ![]() ABC vuông tại A, gọi BM là tia phân giác của
ABC vuông tại A, gọi BM là tia phân giác của ![]() ,
, ![]() . Trên tia BC lấy điểm H sao cho: BA = BH.
. Trên tia BC lấy điểm H sao cho: BA = BH.
a/ Chứng minh: ![]() ABM =
ABM = ![]() HBM
HBM
b/ Chứng minh: MH ![]() BC.
BC.
c/ Tia BA cắt tia HM tại K. Chứng minh ![]() KMC cân tại M.
KMC cân tại M.
d/ Chứng minh: AH // KC
Bài 3: Cho![]() ABC nhọn, kẻ AH vuông góc với BC (H
ABC nhọn, kẻ AH vuông góc với BC (H![]() BC). Cho biết AC=20 cm, AH =12cm, BH = 5cm. Tính độ dài cạnh HC, BC, AB.
BC). Cho biết AC=20 cm, AH =12cm, BH = 5cm. Tính độ dài cạnh HC, BC, AB.
Bài 4: Cho ![]() ABC cân tại A kẻ AH
ABC cân tại A kẻ AH![]() BC (H
BC (H![]() BC)
BC)
a) Chứng minh: HB = HC.
b) Kẻ HD![]() AB (D
AB (D![]() AB), HE
AB), HE![]() AC (E
AC (E![]() AC). Chứng minh
AC). Chứng minh ![]() HDE cân.
HDE cân.
c) Chứng minh BC // DE.
Bài 5: a) Cho ![]() ABC vuông tại A. Tính độ dài BC biết AB = 7cm; AC = 24cm.
ABC vuông tại A. Tính độ dài BC biết AB = 7cm; AC = 24cm.
b) Cho ![]() EDF cân tại D có
EDF cân tại D có ![]() . Tính số đo của góc E.
. Tính số đo của góc E.
Bài 6: Cho tam giác ABC cân tại A, lấy điểm H là trung điểm của đoạn thẳng BC.
a) Chứng minh ![]() ABH =
ABH = ![]() ACH.
ACH.
b) Tia phân giác của góc ABC cắt đoạn AH tại M. Chứng minh: ![]() và
và ![]() MBC cân.
MBC cân.
c) Đường thẳng đi qua A và song song với BC cắt tia BM tại N. Chứng minh: AB = AN.
d) Chứng minh: MC ^ CN.
Bài 7: a) Cho ![]() ABC vuông tại A. Tính độ dài BC biết AB = 8cm; AC = 15cm.
ABC vuông tại A. Tính độ dài BC biết AB = 8cm; AC = 15cm.
b) Cho ![]() EDF cân tại E có
EDF cân tại E có ![]() . Tính số đo của góc E.
. Tính số đo của góc E.
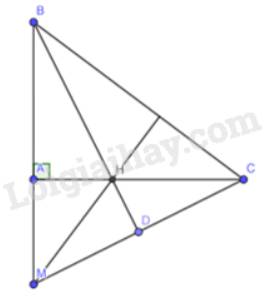
Bài 8: Cho tam giác ABC cân tại A (AB > BC), lấy điểm M là trung điểm của đoạn BC.
a) Chứng minh ![]() ABM =
ABM = ![]() ACM.
ACM.
b) Tia phân giác của góc ACB cắt đoạn AM tại I. Chứng minh: ![]() và
và ![]() IBC cân .
IBC cân .
c) Đường thẳng đi qua B và song song với AC cắt tia CI tại H. Chứng minh: BH = BC.