chứng tỏ đường thẳng -mx + 2y = m+3 luôn đi qua điểm cố định. Xác định tọa độ I
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 10 2019
Giả sử ( x 0 ; y 0 ) là điểm cố định mà đường thẳng mx + 3 + (3m – 1)y = 0 luôn đi qua.
Ta có:
m x 0 + 3 + (3m - 1) y 0 = 0 với mọi m
⇔ m x 0 + 3 + 3m y 0 - y 0 = 0 với mọi m
⇔ m( x 0 + 3 y 0 ) + 3 - y 0 = 0 với mọi m
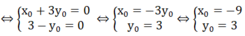
Vậy điểm cố định mà đường thẳng luôn đi qua là (-9: 3)
CM
6 tháng 8 2019
Chứng minh họ đường thẳng y = mx + (2m + 1) (1) luôn đi qua một điểm cố định nào đó.
Giả sử điểm A( x o ; y o ) là điểm mà họ đường thẳng (1) đi qua với mọi m. Khi đó tọa độ điểm A nghiệm đúng phương trình hàm số (1).
Với mọi m, ta có: y o = m x o + (2m + 1) ⇔ ( x o + 2)m + (1 – y) = 0
Vì phương trình nghiệm đúng với mọi giá trị của m nên tất cả các hệ số phải bằng 0.
Suy ra: x o + 2 = 0 ⇔ x o = -2
1 – y o = 0 ⇔ y o = 1
Vậy A(-2; 1) là điểm cố định mà họ đường thẳng y = mx + (2m + 1) luôn đi qua với mọi giá trị m.
15 tháng 7 2021
gọi điểm có tọa độ mà đường thăng y=mx+(3m-1) luôn đi qua
là \(M\left(x0,y0\right)\)
=>x0,y0 thỏa mãn y=mx+(3m-1)
\(=>y0=mx0+3m-1\)
\(< =>mx0+3m-1-y0=0\)
\(< =>m\left(x0+3\right)-\left(y0+1\right)=0\)
\(=>\left\{{}\begin{matrix}x0+3=0\\y0+1=0\end{matrix}\right.< =>\left\{{}\begin{matrix}x0=-3\\y0=-1\end{matrix}\right.\)
vậy đường thăng y=mx+(3m-1) luôn đi qua M(-3;-1) cố định
6 tháng 9 2021
Gọi 2 điểm cố định là \(A\left(x_0;y_0\right)\)
Thay vào ptđt (d) ta được : \(y_0=mx_0+m+1\Leftrightarrow mx_0+m+1-y_0=0\)
\(\Leftrightarrow m\left(x_0+1\right)+\left(1-y_0\right)=0\)
Đẳng thức xảy ra khi \(\hept{\begin{cases}x_0+1=0\\1-y_0=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=1\end{cases}}\Rightarrow A\left(-1;1\right)\)
Vậy d luôn đi qua 1 điểm cố định A(-1;1)
6 tháng 9 2021
Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình :
14.x2=x−114.x2=x−1
<=> x2 = 4x - 4
<=> x2 - 4x + 4 = 0 <=> (x - 2)2 = 0 <=> x - 2= 0 <=> x = 2
=> y = 2-1 = 1
Vậy (P) cắt (d) tại 1 điểm duy nhất là (2;1)
=> đpcm
đúng ko ?????????????
sai thì cho mik xin lỗi
15 tháng 12 2022
y=m(x-2)+1
=>m(x-2)-y+1=0
Điểm mà (d) luôn đi qua có tọa độ là:
x-2=0 và 1-y=0
=>x=2 và y=1
Lời giải:
Gọi $I(x_0,y_0)$ là điểm cố định mà đường thẳng đã cho luôn đi qua.
Điều đó có nghĩa là:
$-mx_0+2y_0=m+3$ với mọi $m$
$\Leftrightarrow m(-x_0-1)+(2y_0-3)=0$ với mọi $m$
\(\Rightarrow \left\{\begin{matrix} -x_0-1=0\\ 2y_0-3=0\end{matrix}\right.\Rightarrow \left\{\begin{matrix} x_0=-1\\ y_0=\frac{3}{2}\end{matrix}\right.\)
Vậy $I(-1; \frac{3}{2})$