Cho tam giac ABC có AB=AC=5cm;BC=6cm.Kẻ BH vuông góc với AC(H thuộc AC) và CK vuông góc với Ab(K thuộc AB). Gọi giao điểm của BH và CK là D. Lấy M là trung điểm của BC.Cmr A,D,M thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(3^2+4^2=5^{2^{ }}\)
=> \(AB^2+AC^2=BC^2\)
=> Tam giác ABC vuông tại A
( Định lí Pi-ta-go đảo )
Chúc bn hok tốt

Áp dụng định lí Py-ta-go trong tam giác ABC
Ta có: 32+42=9+16=25(cm)
=>BC=\(\sqrt{25}\)=5(cm)
Vậy tam giác ABC là tam giác vuông tại A

Các cạnh của tam giác DEF là
DE = 5cm
DF = 6cm
EF =8cm k mik nha

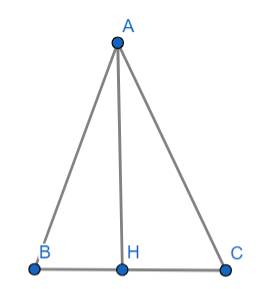
Xét tam giác vuông ABH vuông tại H ta có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}\)
\(\Rightarrow AH=\sqrt{6^2-5^2}=\sqrt{11}\left(cm\right)\)
Mà tam giác ABC cân tại A nên \(BC=2BH=2\cdot5=10\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot10\cdot\sqrt{11}=5\sqrt{11}\left(cm^2\right)\)

A B C H
Tính \(AH\): dùng pytago với \(\Delta ABH\)
Tính \(HC\): dùng trừ đoạn
Tính \(AC\): đã có \(AH;HC\)thì dùng pytago với \(\Delta ACH\)

b) Ta có: BAAD=CACE=12BAAD=CACE=12
⇒ BC // DE ( 2 )
Từ ( 1) và ( 2) có: DE // BC (cmt) và DI // BC (cmt)
Ta thấy qua điểm D nằm ngoài BC kẻ được 2 đường thẳng song song với BC, điều này trái với tiên đề Ơ-clít nên hai đường thẳng DE và DI phải trùng nhau
⇒ D, I, E cùng nằm trên một đường thẳng
⇒ D, I, E thẳng hàng
Bạn ơi mình làm phần b thôi nhé

Nếu tam giác vuông tại A thì: AB2 + AC2 = BC2
Gọi AC là x, ta có: x2 + (2x)2 = BC2
<=> x2 + 4x2 = 52
<=> 5x2 = 25
<=> x2 = 5
<=> x = \(\sqrt{5}\) = AC


bài này pk áp dụng định lí PYTAGO j đó , lớp mk chưa hc nên bn kham khảo hình