cứu mình vớiiii gấp ạ 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


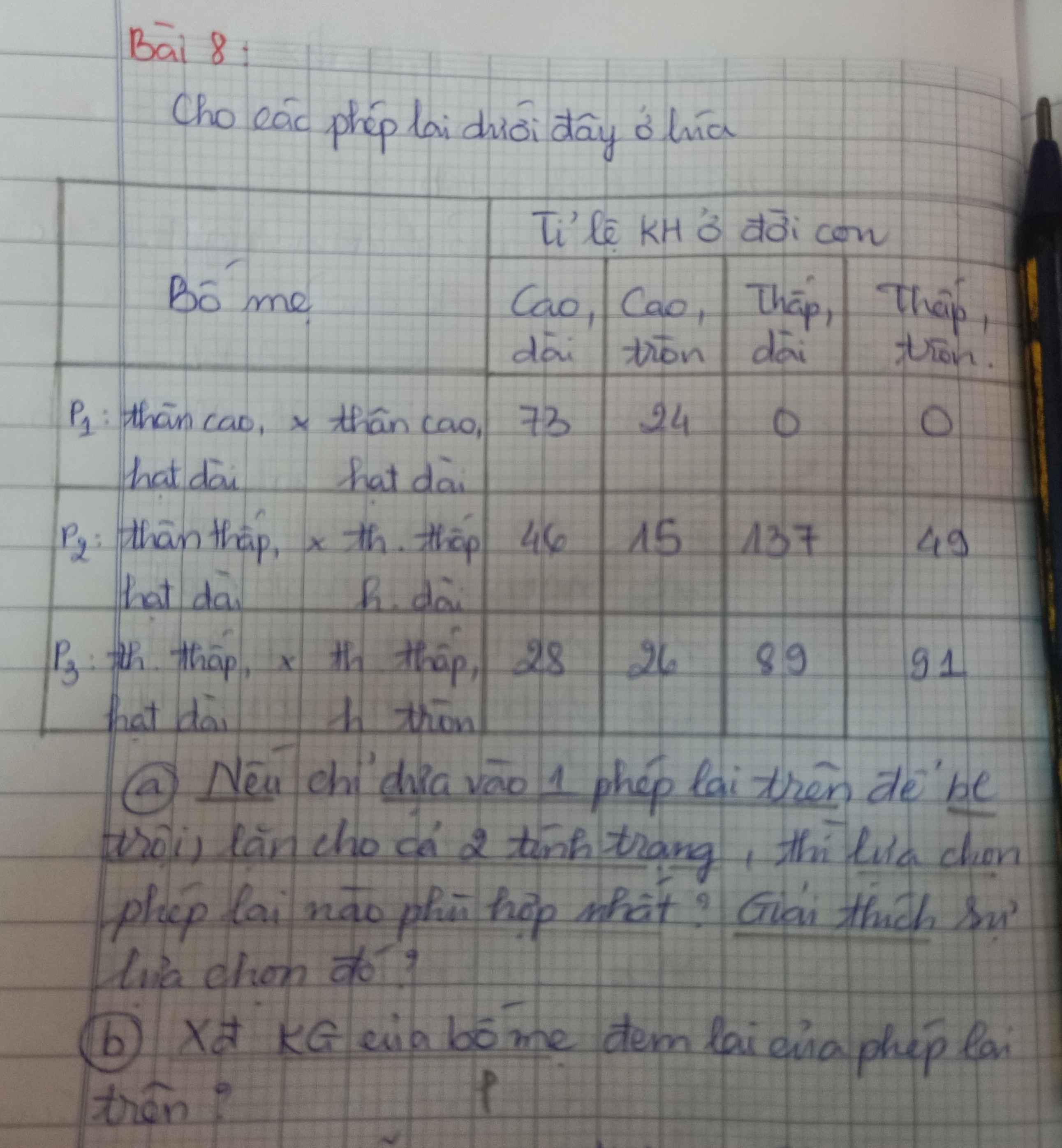
a) Xét phép lai thứ hai: thu được:
137 thấp,dài: 46 cao,dài: 49 thấp, tròn:15 cao tròn
Xét tính trạng hình dạng cây:\(\dfrac{thấp}{cao}=\dfrac{137+49}{46+15}=\dfrac{3}{1}\)
=> Tính trạng thấp trội hoàn toàn so với tính trạng cao
Xét tính trạng hình dạng quả: \(\dfrac{Dài}{Tron}=\dfrac{137+46}{49+15}=\dfrac{3}{1}\)
=> Tính trạng dài THT so với tính trạng tròn
=> Lựa chọn phép lai đó vì khi nhìn ta sẽ thấy nó tuân theo tỉ lệ 9:3:3:1( Quy luật phân li độc lập của Menden)
Quy ước gen: A thấp. a cao
B dài. b tròn
b) Xét phép lai 1:Thân cao, dài x thân cao,dài
F1 thu dc: 73 cao,dài: 24 cao, tròn ~3:1
=> có 4 tổ hợp giao tử => mỗi bên P cho ra 2 loại giao tử
Vì kiểu hình của P toàn là thân cao => P: A_
vì kiểu hình của P toàn là hạt dài mà thu dc lại có hạt tròn => P: Bb
=> kiểu gen của P: AABb x AABb
P: AABb( thấp, dài) x AABb( thấp, dài)
Gp AB,Ab AB,Ab
F1: 1AABB:2AABb:1AAbb
kiểu hình: 3 cao dài: 1 cao,tròn
Xét phép lai 2:P : thấp,dài x thấp,dài
F1: 46 cao,dài:15 cao,tròn:137 thấp, dài:49 thấp, tròn
~ 3:1:9:3 hay 9:3:3:1
=> Tuân theo quy luật phân tính của Menden
=> P dị hợp hai cặp tính trạng => kiểu gen P: AaBb
P: AaBb( thấp, dài) x AaBb( thấp,dài)
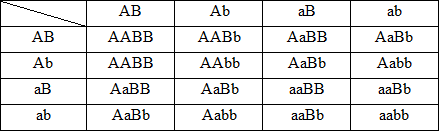
Kiểu gen: 9A_B_:3 A_bb:3aaB_:1aabb
Kiểu hình: 9 thấp,dài: 3 thấp,tròn:3 cao,dài:1 cao,tròn
Xét phép lai 3: P: thấp,dài x thấp ,tròn
F1:28 cao,dài:26 cái,tròn:89 thấp dài:91 thấp tròn
~ 1:1:3:3 =(1:1)(3:1)
=> có 8 tổ hợp giao tử
\(\left\{{}\begin{matrix}Xet.tinh.trang.hinh.dang.cay\left(1:1\right):Aa.aa\\xet.tinh.trang.hinh.dang.hat\left(3:1\right):Bb.Bb\end{matrix}\right.\)
=> kiểu gen P: AaBb x aaBb hay Aabb x AaBb
Mà kiểu hình của P:thấp,dài x thấp tròn
=> kiểu gen P: Aabb x AaBb
P: Aabb( thấp, tròn) x AaBb( thấp, dài)
Gp Ab,ab AB,Ab,aB,ab
F1: 1AABb:1 AAbb:1AaBb:1Aabb:1AaBb:1Aabb:1aaBb:1aabb
kiểu gen: 3A_B_:3A_bb:1aaB_:1aabb
kiểu hình: 3thấp, dài:3 thấp,tròn:1 cao,dài:1 cao,tròn

3:
độ dài cạnh là \(\sqrt{\dfrac{54}{6}}=\sqrt{9}=3\left(m\right)\)
V=3^3=27m3


Gọi các phân số cần tìm là: \(\dfrac{a}{b}\) theo bài ra ta có:
\(\dfrac{a}{b}\) = \(\dfrac{a+2}{b\times2}\)
a.(b x 2) = (a + 2) x b
ab x 2 = ab + 2b
ab = 2b
a = 2
Ta có: \(\dfrac{2}{b}\) > \(\dfrac{1}{5}\) = \(\dfrac{2}{10}\)
⇒ b < 10 ⇒ b = 1; 2; 3; 4; 5; 6; 7; 8; 9
Vì \(\dfrac{2}{b}\) không phải là số tự nhiên nên b \(\in\) {3; 4; 5; 6; 7; 8; 9}
Bài 16:
\(\dfrac{1}{6}\) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + \(\dfrac{1}{7^2}\) +...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\)
\(\dfrac{1}{5^2}\) < \(\dfrac{1}{4.5}\) = \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\)
\(\dfrac{1}{6^2}\) < \(\dfrac{1}{5.6}\) = \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\)
............................
\(\dfrac{1}{100^2}\) < \(\dfrac{1}{99.100}\) = \(\dfrac{1}{99}\) - \(\dfrac{1}{100}\)
Cộng vế với vế ta có:
\(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\)+...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\) - \(\dfrac{1}{100}\) < \(\dfrac{1}{4}\) (1)
\(\dfrac{1}{5^2}\) > \(\dfrac{1}{5.6}\) = \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\)
\(\dfrac{1}{6^2}\) > \(\dfrac{1}{6.7}\) = \(\dfrac{1}{6}\) - \(\dfrac{1}{7}\)
...............................
\(\dfrac{1}{100^2}\) > \(\dfrac{1}{100.101}\) = \(\dfrac{1}{100}\) - \(\dfrac{1}{101}\)
Cộng vế với vế ta có:
\(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + ... + \(\dfrac{1}{100^2}\) > \(\dfrac{1}{5}\) - \(\dfrac{1}{101}\)= \(\dfrac{96}{505}\) > \(\dfrac{96}{576}\) = \(\dfrac{1}{6}\) (2)
Kết hợp (1) và (2) ta có:
\(\dfrac{1}{6}\) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) +...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\) (đpcm)


Bài 1:
Theo đề, ta có:
\(\left\{{}\begin{matrix}-3\cdot\left(-2\right)^2+b\cdot\left(-2\right)+c=-1\\-3\cdot1^2+b\cdot1+c=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2b+c-12=-1\\b+c-3=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2b+c=11\\b+c=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3b=3\\b+c=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-1\\c=9\end{matrix}\right.\)

\(A=\sqrt{3-\sqrt{5}}-\sqrt{4-\sqrt{15}}+\sqrt{6-3\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\sqrt{6-2\sqrt{5}}-\sqrt{8-2\sqrt{15}}+\sqrt{12-6\sqrt{3}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{5}-1-\sqrt{5}+\sqrt{3}+3-\sqrt{3}\right)\)
=2/căn 2=căn 2
\(B=\sqrt{4-\sqrt{7}}-\sqrt{14-5\sqrt{3}}-\sqrt{5+\sqrt{21}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{8-2\sqrt{7}}-\sqrt{28-10\sqrt{3}}-\sqrt{10+2\sqrt{21}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{7}-1-5+\sqrt{3}-\sqrt{7}-\sqrt{3}\right)\)
=-6/căn 2=-3căn2
\(C=\sqrt{11-6\sqrt{2}}-\sqrt{6-4\sqrt{2}}+\sqrt{7-2\sqrt{6}}\)
=3-căn 2-2+căn 2+căn 6-1
=căn 6
\(D=\sqrt{6-\sqrt{11}}-\sqrt{10+3\sqrt{11}}+2\sqrt{2}-1\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{12-2\sqrt{11}}-\sqrt{20+6\sqrt{11}}\right)+2\sqrt{2}-1\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{11}-1-\sqrt{11}-3\right)+2\sqrt{2}-1\)
=-1
\(F=\sqrt{6+3\sqrt{3}}-\sqrt{2+\sqrt{3}}+\sqrt{6-4\sqrt{2}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{12+6\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)+2-\sqrt{2}\)
=1/căn 2(3+căn 3-căn 3-1)+2-căn 2
=căn 2+2-căn 2
=2

 cứu tớ vớiiii
cứu tớ vớiiii

 Cứu mình gấp ạ!!! Mình sắp thi rồi!!!
Cứu mình gấp ạ!!! Mình sắp thi rồi!!!


1 You must cover all electrical sockets because electricity can kill
2 Bell started experimenting with ways of transmitting speech over a long distance
VII
33 Tim to go to bed soon
34 her students to do all exercises before going to school
35 interested in sending greeting card....
36 going to travel around America next month