Cho hai hàm số y=2x-4(d) và y=-x+4(d').so sánh góc B tạo bởi đường thẳng (d) với trục Ox và góc A tạo bởi đường thẳng (d') với trục Ox
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 12 2023
a:
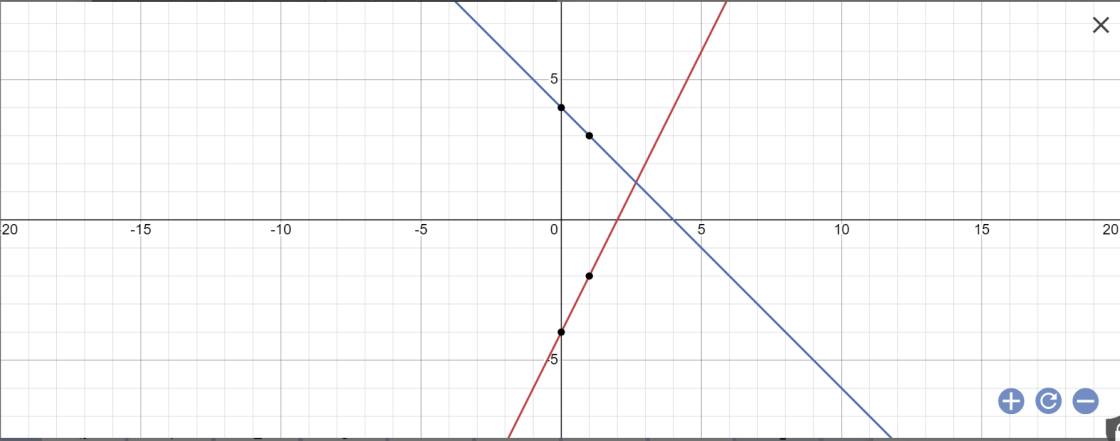
b: Tọa độ điểm Q là:
\(\left\{{}\begin{matrix}2x-4=-x+4\\y=-x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=8\\y=-x+4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{8}{3}\\y=-\dfrac{8}{3}+4=\dfrac{4}{3}\end{matrix}\right.\)
Vậy: \(Q\left(\dfrac{8}{3};\dfrac{4}{3}\right)\)
Tọa độ M là:
\(\left\{{}\begin{matrix}x=0\\y=2x-4=2\cdot0-4=-4\end{matrix}\right.\)
Vậy: M(0;-4)
Tọa độ N là:
\(\left\{{}\begin{matrix}x=0\\y=-x+4=-0+4=4\end{matrix}\right.\)
vậy: N(0;4)
Q(8/3;4/3); M(0;-4); N(0;4)
\(QM=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(-4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{5}}{3}\)
\(QN=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{2}}{3}\)
\(MN=\sqrt{\left(0-0\right)^2+\left(4+4\right)^2}=8\)
Xét ΔMNQ có
\(cosMQN=\dfrac{QM^2+QN^2-MN^2}{2\cdot QM\cdot QN}=\dfrac{-1}{\sqrt{10}}\)
=>\(\widehat{MQN}\simeq108^026'\)
\(sinMQN=\sqrt{1-cos^2MQN}=\dfrac{3}{\sqrt{10}}\)
Diện tích tam giác MQN là:
\(S_{MQN}=\dfrac{1}{2}\cdot QM\cdot QN\cdot sinMQN\)
\(=\dfrac{1}{2}\cdot\dfrac{3}{\sqrt{10}}\cdot\dfrac{8\sqrt{5}}{3}\cdot\dfrac{8\sqrt{2}}{3}=\dfrac{32}{3}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
23 tháng 12 2022
a, Vẽ đồ thị hàm số y = 2x - 4
- Giao đồ thị với trục Ox là điểm có tung độ bằng 0 ; y = 0
=> 2x - 4 = 0 => x = 4/2 => x= 2
Đồ thị cắt trục hành tại A ( 2; 0)
- Giao đồ thị với trục Oy là điểm cs hoành độ bằng 0 ; x = 0
=> y = 0-4 = -4
Đồ thị cắt trục tung tại B ( 0; -4)
Tính khoảng cách từ điểm O đến đt (d) : y = 2x - 4
=> 2x - 4 - y = 0
=> 2x - y - 4 = 0 (d1)
Khoảng cách từ O đến d chính là khoảng cách từ O đến (d1)
Điểm O(0 ;0)
d(0; d1) = \(\dfrac{|2.0-0-4|}{\sqrt{2^2+1^1}}\)
d(O; d1) = \(\dfrac{4}{\sqrt{5}}\) = \(\dfrac{4\sqrt{5}}{5}\)
b, phương trình đt d' có dạng : ax + b
d'//d \(\Leftrightarrow\) a = 2; b # -4
Phương trình đt d' có dạng : 2x + b
Vì d' đi qua A ( 0; 3) nên tọa độ điểm A thỏa mãn pt đường thẳng d.
Thay tọa độ điểm A vào pt đt d' ta có :
2. 0 + b = 3
0 + b = 3
b = 3
vậy các hệ số a; b của đt d' son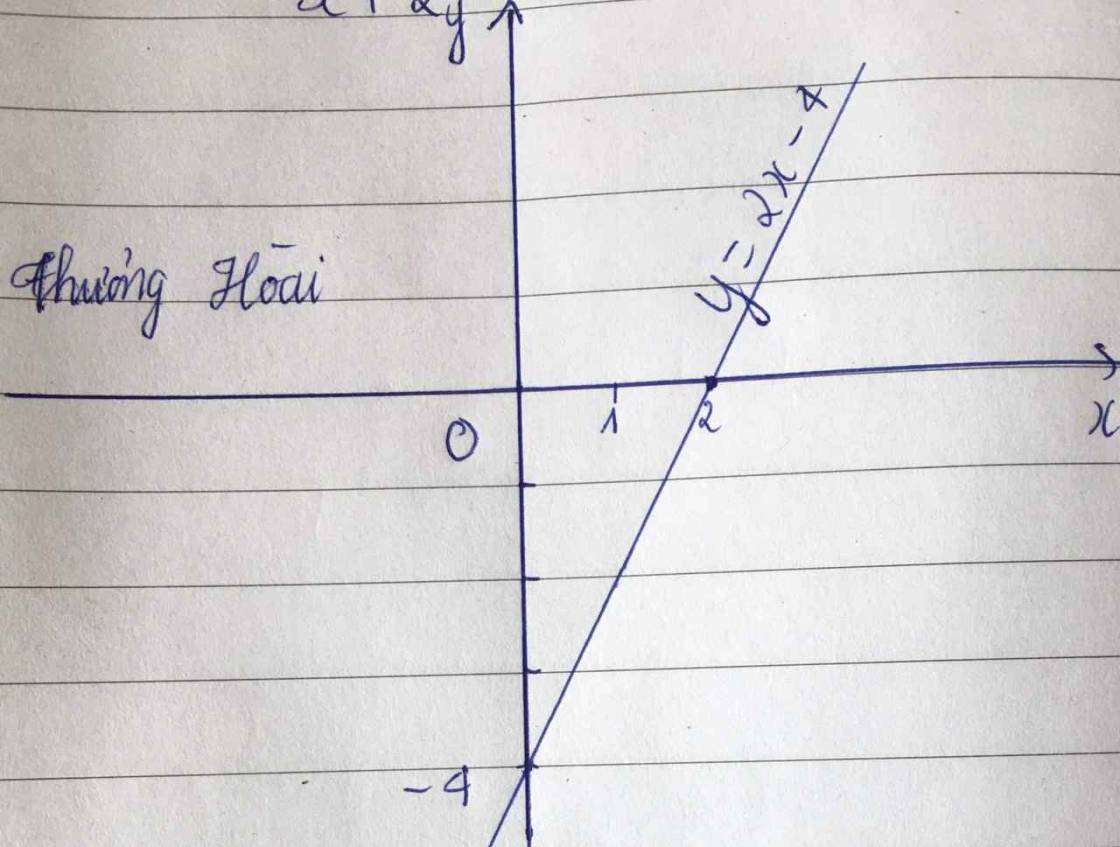
g song với d và đi qua A( 0; 3) lần lượt là : 2; 3
6 tháng 1 2022
a: k=xy=5x2=10
b: Thay x=3 vào y=3x, ta được:
y=3x3=9
Vậy: điểm A(3;9) thuộc đồ thị y=3x
c: f(4)=16-1=15
KC
6 tháng 1 2022
a, Vì 2 đại lượng x và y tỉ lệ nghịch với nhau
⇒ x . y = a (a ≠ 0)
Khi x = 2 thì y = 5
⇒ 2 . 5 = a ⇒ a = 10
Vậy hệ số tỉ lệ của y đối với x là 10
b, x . y = 10 ⇒ y = \(\dfrac{10}{x}\)
c, x . y = 10
x = 5 ⇒ y = 10 : 5 = 2
x = -10 ⇒ y = 10 : (-10) = -1
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Hàm số ở câu a) \(y = 9{x^2} + 5x + 4\) là hàm số bậc hai với \(a = 9,b = 5,c = 4\)
Hàm số ở câu b), c) không phải là hàm số bậc hai vì chứa \({x^3}\)
Hàm số ở câu d) \(y = 5{x^2} + \sqrt x + 2\) không phải là hàm số bậc hai vì chứa \(\sqrt x \)
GA
1
5 tháng 3 2022
a: Để hai đường song song thì m+2=4
hay m=2
b: Tọa độ giao điểm của y=-3x+4 và y=2x-1 là:
\(\left\{{}\begin{matrix}-3x+4=2x-1\\y=2x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
Thay x=1 và y=1 vào (d), ta được:
m+2+m-3=1
=>2m-1=1
hay m=1
5 tháng 12 2023
a: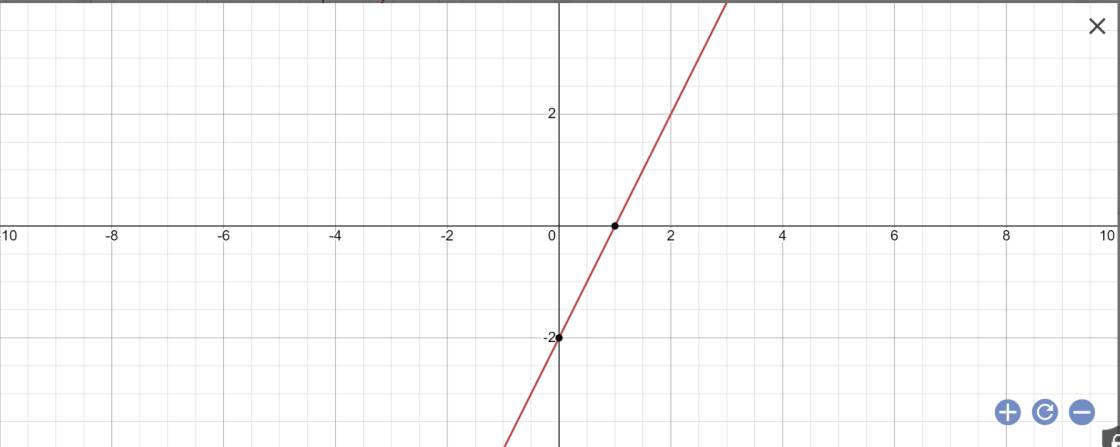 
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}m+1=2\\6< >-2\left(đúng\right)\end{matrix}\right.\)
=>m+1=2
=>m=1
c:
(d'): y=(m+1)x+6
=>(m+1)x-y+6=0
Khoảng cách từ O đến (d') là:
\(d\left(O;\left(d'\right)\right)=\dfrac{\left|0\cdot\left(m+1\right)+0\cdot\left(-1\right)+6\right|}{\sqrt{\left(m+1\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}\)
Để \(d\left(O;\left(d'\right)\right)=3\sqrt{2}\) thì \(\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}=3\sqrt{2}\)
=>\(\sqrt{\left(m+1\right)^2+1}=\sqrt{2}\)
=>\(\left(m+1\right)^2+1=2\)
=>\(\left(m+1\right)^2=1\)
=>\(\left[{}\begin{matrix}m+1=1\\m+1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-2\end{matrix}\right.\)