cho góc xOy khác góc bẹt,Oz là tia phân giác trên các tia Ox,Oy lần lượt lấy các điểm AB sao cho OA=OB.C là điểm nằm trên tia Oz.Gọi D là giao điểm của AC và tia Oy,E là giao điểm của BC và tia Ox.Chứng minh
a,AC=BC
b,tam giác ACE = tam giác BCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 2 2021
Giải:
Hình bạn tự vẽ nhé.
a) Xét tam giác BDO và tam giác ACO có:
OD = OC (gt)
Góc O chung
AO = BO (gt)
=> Tam giác ACO = tam giác BDO (c.g.c) (đpcm)
b) Ta có: BO = AO (gt)
CO = DO (gt)
=> CO - BO = DO - AO
=> BC = AD
Vì tam giác BDO = tam giác ACO (chứng minh trên)
nên góc BDO = góc ACO (2 góc tương ứng) hay góc ADI = góc BCI
góc DBO = góc CAO (2 góc tương ứng)
Mà góc DBO + góc CBD = góc CAO + góc CAD = 180o
=> Góc CBD = góc CAD hay góc CBI = góc DAI
Xét tam giác BCI và tam giác ADI có:
Góc CBI = góc DAI (chứng minh trên)
BC = AD (chứng minh trên)
Góc BCI = góc ADI (chứng minh trên)
=> Tam giác BCI = tam giác ADI (g.c.g)
=> AI = BI (2 cạnh tương ứng) (đpcm)
c) Ta có: tam giác BCI = tam giác ADI (chứng minh trên)
=> CI = DI (2 cạnh tương ứng)
Xét tam giác DIO và tam giác CIO có:
OI cạnh chung
DO = CO (gt)
CI = DI (chứng minh trên)
=> Tam giác CIO = tam giác DIO (c.c.c)
=> Góc DOI = góc COI (2 góc tương ứng)
hay góc IOx = góc IOy
Mà OI là tia nằm giữa 2 tia Ox, Oy
=> OI là tia phân giác của góc xOy (đpcm)
CM
10 tháng 11 2017
ΔAEB = ΔCED ⇒ EA = EC (hai cạnh tương ứng)
ΔOAE và ΔOCE có
OA = OC
EA = EC
OE cạnh chung
⇒ ΔOAE = ΔOCE (c.c.c)
⇒ 
(hai góc tương ứng)
Vậy OE là tia phân giác của góc xOy.
10 tháng 1 2022
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOBC
nên \(\widehat{OAD}=\widehat{OBC}\)
\(\Leftrightarrow180^0-\widehat{OAD}=180^0-\widehat{OBC}\)
hay \(\widehat{EAB}=\widehat{ECD}\)
Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó: ΔEAB=ΔECD
c: Ta có: ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy
29 tháng 12 2021
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
CM
3 tháng 1 2019
Ta có: ΔOIA và ΔOIC có
OI chung
IA = IC (chứng minh trên)
OA = OC (giả thiết)
ΔOIA = ΔOIC (c.c.c)
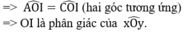
a) Xét \(\Delta OAC\)và \(\Delta OBC\)có:
OA = OB (gt)
\(\widehat{AOC}=\widehat{BOC}\)(Oz là tia p/g của \(\widehat{xOy}\))
OC là cạnh chung
\(\Rightarrow\Delta OAC=\Delta OBC\left(c.g.c\right)\)
\(\Rightarrow AC=BC\)(2 cạnh tương ứng)
b) Ta có: \(\Delta OAC=\Delta OBC\)(theo a)
\(\Rightarrow\widehat{OAC}=\widehat{OBC}\)(2 góc tương ứng)
hay \(\widehat{OAD}=\widehat{OBE}\)
Xét \(\Delta OAD\)và \(\Delta OBE\)có:
\(\widehat{O}\)là góc chung
OA = OB (gt)
\(\widehat{OAD}=\widehat{OBE}\)(cmt)
\(\Rightarrow\Delta OAD=\Delta OBE\left(g.c.g\right)\)
=> AD = BE (2 cạnh tương ứng)
Mà AC = BC (theo a)
=> AD - AC = BE - BC
=> CD = CE
Xét \(\Delta ACE\)và \(\Delta BCD\)có:
AC = BC (cmt)
\(\widehat{ACE}=\widehat{BCD}\)(2 góc đối đỉnh)
CE = CD (cmt)
\(\Rightarrow\Delta ACE=\Delta BCD\left(c.g.c\right)\)
hình đâu bạn ei