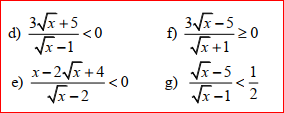Giải bpt
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 10 2021
d: Để A<0 thì \(\sqrt{x}-1< 0\)
hay \(0\le x< 1\)
f: Để \(B\ge0\) thì \(3\sqrt{x}-5\ge0\)
hay \(x\ge\dfrac{25}{9}\)
28 tháng 7 2023
c) \(\dfrac{x+5}{x^2-5x}-\dfrac{x-5}{2x^2+10x}=\dfrac{x+25}{2x^2-50}\)
\(\Leftrightarrow\dfrac{x+5}{x\left(x-5\right)}-\dfrac{x-5}{2x\left(x+5\right)}=\dfrac{x+25}{2\left(x^2-25\right)}\)
\(\Leftrightarrow\dfrac{2\left(x+5\right)\left(x-5\right)}{2x\left(x+5\right)\left(x-5\right)}-\dfrac{\left(x-5\right)^2}{2x\left(x+5\right)\left(x-5\right)}=\dfrac{\left(x+25\right)x}{2x\left(x+5\right)\left(x-5\right)}\)
\(\Leftrightarrow2\left(x^2-25\right)-\left(x^2-10x+25\right)=x^2+25x\)
\(\Leftrightarrow2x^2-50-x^2+10x-25=x^2+25x\)
\(\Leftrightarrow2x^2-x^2-x^2+10x-25x=50+25\)
\(\Leftrightarrow-15x=75\)
\(\Leftrightarrow x=\dfrac{75}{-15}\)
\(\Leftrightarrow x=-5\)
HP
20 tháng 2 2021
e, ĐK: \(x\ne2\)
\(\dfrac{3}{x-2}>1\Leftrightarrow\dfrac{5-x}{x-2}>0\)
\(\Leftrightarrow\left\{{}\begin{matrix}5-x>0\\x-2>0\end{matrix}\right.\left(1\right)\) hoặc \(\left\{{}\begin{matrix}5-x< 0\\x-2< 0\end{matrix}\right.\left(2\right)\)
\(\left(1\right)\Leftrightarrow2< x< 5\)
\(\left(2\right)\Leftrightarrow\) vô nghiệm
Vậy \(2< x< 5\)
f, ĐK: \(x\ne\dfrac{1}{2}\)
\(\dfrac{2x^2+x}{1-2x}\ge1-x\)
\(\Leftrightarrow\dfrac{2x^2+x+\left(x-1\right)\left(1-2x\right)}{\left(1-2x\right)\left(x-1\right)}\ge0\)
\(\Leftrightarrow\dfrac{4x-1}{\left(1-2x\right)\left(x-1\right)}\ge0\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x-1\ge0\\\left(1-2x\right)\left(x-1\right)>0\end{matrix}\right.\left(1\right)\) hoặc \(\left\{{}\begin{matrix}4x-1\le0\\\left(1-2x\right)\left(x-1\right)< 0\end{matrix}\right.\left(2\right)\)
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{4}\\\dfrac{1}{2}< x< 1\end{matrix}\right.\Leftrightarrow\dfrac{1}{2}< x< 1\)
\(\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{1}{4}\\\left[{}\begin{matrix}x>1\\x< \dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow x\le\dfrac{1}{4}\)
Vậy ...
MH
5 tháng 2 2022
\(\dfrac{x+1}{x+2}-\dfrac{5}{x-2}=\dfrac{20}{4-x^2}\) (\(ĐK:x\)≠\(2;-2\))
⇔ \(\dfrac{\left(x+1\right)\left(x-2\right)-5\left(x+2\right)}{x^2-4}=\dfrac{20}{4-x^2}\)
⇔ \(-\left(x+1\right)\left(x-2\right)+5\left(x+2\right)=20\)
⇔ \(-\left(x^2-2x+x-2\right)+5x+10=20\)
⇔ \(-x^2+x+2+5x+10-20=0\)
⇔ \(-x^2+6x-8=0\)
⇔ \(-\left(x^2-6x+9\right)=-1\)
⇔ \(\left(x-3\right)^2=1\)
⇔ \(\left[{}\begin{matrix}x-3=1\\x-3=-1\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)
Vậy ...
5 tháng 2 2022
b: \(\Leftrightarrow20-5\left(3x+2\right)>4\left(x+7\right)\)
=>20-15x-10>4x+28
=>-15x+10-4x-28>0
=>-19x-18>0
=>-19x>18
hay x<-18/19
21 tháng 6 2023
=>x^2=5x hoặc x^2=-5x
=>x(x-5)=0 hoặc x(x+5)=0
=>x=0;x=5;x=-5
LH
1
VQ
26 tháng 4 2019
1) ĐKXĐ: \(\left[{}\begin{matrix}x\le1\\x\ge2\end{matrix}\right.\)
ta có: (-6).\(\sqrt{6x^2-18x+12}\) > \(6x^2-18x-60\)
⇔ \(6x^2-18x+12\) + \(2.3.\sqrt{6x^2-18x+12}+9-81\) > 0
⇔ \(\left(\sqrt{6x^2-18x+12}+3\right)^2-9^2\) > 0
⇔ \(\left(\sqrt{6x^2-18x+12}+12\right).\left(\sqrt{6x^2-18x+12}-6\right)\) > 0
⇔ \(\sqrt{6x^2-18x+12}-6\) > 0
⇔ \(\sqrt{6x^2-18x+12}>6\)
⇔\(6x^2-18x+12>36\)
⇔ \(6x^2-18x-24>0\)
⇔\(\left[{}\begin{matrix}x< -1\\x>4\end{matrix}\right.\)
đối chiếu ĐKXĐ ban đầu ta được: x ϵ (-∞;-1) \(\cup\)(4;+∞)
b) ĐKXĐ: \(\forall x\) ϵ R
\(\left(x-2\right)\sqrt{x^2+4}-\left(x-2\right)\left(x+2\right)\le0\)
⇔\(\left(x-2\right)\left(\sqrt{x^2+4}-x-2\right)\le0\)
⇔\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge2\\\sqrt{x^2+4}-x-2\le0\end{matrix}\right.\\\left\{{}\begin{matrix}x\le2\\\sqrt{x^2+4}-x-2\ge0\end{matrix}\right.\end{matrix}\right.\)⇔ \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge2\\x^2+4\le x^2+4x+4\end{matrix}\right.\\\left\{{}\begin{matrix}x\le2\\x^2+4\ge x^2+4x+4\end{matrix}\right.\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge2\\x\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x\le2\\x\le0\end{matrix}\right.\end{matrix}\right.\)⇔\(\left[{}\begin{matrix}x\ge2\\x\le0\end{matrix}\right.\)
Đối chiếu ĐKXĐ ta được x ϵ ( -∞;0) \(\cup\)( 2; +∞)
AT
30 tháng 7 2021
\(x^2-1>0\Rightarrow x^2>1\Rightarrow\left|x\right|>1\Rightarrow\left[{}\begin{matrix}x>1\\x< -1\end{matrix}\right.\)
UT
1 tháng 8 2021
Th1
2x+3=x-4(x>=-3/2)
<=>x=-7(loại)
Th2
2x+3=4-x(x=<-3/2)
<=>3x=1
<=>x=1/3(loại)
Pt vô nghiệm
MN
1 tháng 8 2021
\(\left|2x+3\right|=x-4\left(x\ge4\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+3=x-4\\2x+3=4-x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3-4\\3x=4-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-7\left(L\right)\\x=\dfrac{1}{3}\left(L\right)\end{matrix}\right.\)
Không có giá trị của x thỏa mãn.
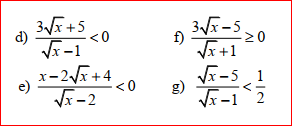
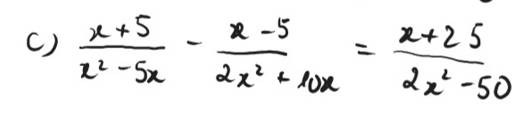
f: Để \(A\ge0\) thì \(3\sqrt{x}-5\ge0\)
hay \(x\ge\dfrac{25}{9}\)