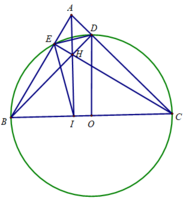
Cho ABC nhọn, đường tròn O bán kính BC cắt AC, AB tại D và E. Gọi giao điểm của BD và CE là H, AH cắt BC tại F.
a) Chứng minh \(AF\perp BC,\widehat{AFD}=\widehat{ACE}\)
b) Gọi M là trung điểm của AM. Chứng minh: \(MD\perp OD\)và 5 điểm M,D,O,F,E thuộc một đường tròn
c) Gọi K là giao điểm của AH và DE. Chứng minh: \(MD^2=MK.MF\) và K là trực tâm của MBC
d) Chứng minh: \(\frac{2}{FK}=\frac{1}{FA}+\frac{1}{FH}\)