phát biểu định lí pytago..và chứng minh
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 6 2017
Sao cậu không tra trên google
Các cách chứng minh định lý pytago là :
Link :
www.bachkhoatrithuc.vn - Các cách chứng minh định lý Pitago,
17 tháng 6 2017
Định lý có thể chứng minh bằng phương pháp đại số khi sử dụng 4 tam giác vuông bằng nhau có các cạnh a, b và c, các tam giác này được sắp xếp thành một hình vuông lớn có cạnh là cạnh huyền c. Các tam giác bằng nhau có diện tích , khi đó hình vuông nhỏ bên trong có cạnh là b − a và diện tích là (b − a)2.
NT
4
KT
22 tháng 7 2018
A B C H
Cho \(\Delta ABC\)có: \(AB^2+AC^2=BC^2\)đường cao \(AH\)
Chứng minh: \(\Delta ABC\)vuông tại A (tức Pytago đảo)
Bài làm
Áp dụng định lý Pytago ta có:
\(AB^2=AH^2+BH^2\)
\(AC^2=AH^2+HC^2\)
Theo giả thiết ta có: \(BC^2=AB^2+AC^2\)
\(\Rightarrow\)\(AH^2=BH.CH\) \(\Rightarrow\)\(\frac{AH}{CH}=\frac{BH}{AH}\)
Xét \(\Delta ABH\)và \(\Delta CAH\)có:
\(\frac{AH}{CH}=\frac{BH}{AH}\) (cmt)
\(\widehat{AHB}=\widehat{CHA}=90^0\)
suy ra: \(\Delta ABH~\Delta CAH\)
\(\Rightarrow\)\(\widehat{BAH}=\widehat{ACH}\)
suy ra: \(\widehat{BAC}=90^0\)
N
22 tháng 7 2018
Trong 1 tam giac vuong co ti le cua 3 canh
Đầu tiên Bình phương của cạnh huyền ,bạn bình phương tỉ số đó lên (rồi đánh số 1 nhỏ)
Sau đó Tổng bình phương 2 cạnh còn lại rồi tính ra công lại bằng số bình phương của cạnh huyền(rồi đánh số 2)
Từ 1 và 2 suy ra:Tổng bình phương cạnh huyền bằng tổng bình phương 2 cạnh góc vuông
Vậy là bạn chứng minh bình thường rồi kết luận định lí của pitago đảo thành pitago.Vậy là xong rồi
11 tháng 11 2023
Nếu Ox,Oy là hai tia phân giác của hai góc kề bù thì Ox\(\perp Oy\)
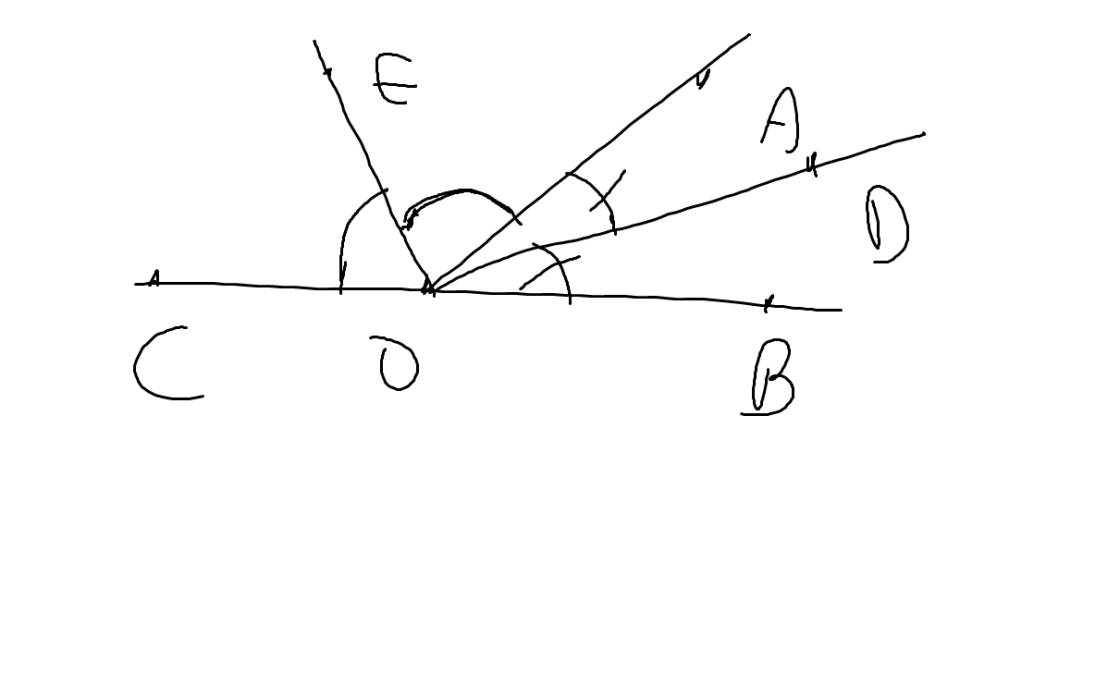
| GT | \(\widehat{AOB};\widehat{AOC}\) là hai góc kề bù OD,OE lần lượt là phân giác của \(\widehat{AOB};\widehat{AOC}\) |
| KL | OD\(\perp\)OE |
OD là phân giác của \(\widehat{AOB}\)
=>\(\widehat{AOB}=2\cdot\widehat{AOD}\)
OE là phân giác của \(\widehat{AOC}\)
=>\(\widehat{AOC}=2\cdot\widehat{AOE}\)
\(\widehat{AOB}+\widehat{AOC}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{AOE}+2\cdot\widehat{AOD}=180^0\)
=>\(\widehat{AOE}+\widehat{AOD}=90^0\)
=>\(\widehat{EOD}=90^0\)
=>OE\(\perp\)OD(ĐPCM)
