X2-6X+9-16=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 3 2020
a)(Sửa đề) \(4(x^2-6x+9)-16(4x^2+28x+49)=0\)
\(⇔(2x-6)^2-(8x+28)^2=0\)
\(⇔(-6x-34)(10x+22)=0\)
\(⇔\left[\begin{array}{} -6x-34=0\\ 10x+22=0 \end{array}\right.\)
\(⇔\left[\begin{array}{} x=-\dfrac{17}{3}\\ x=-\dfrac{11}{5} \end{array}\right.\)
b)(Sửa đề 1) \((2x-16)^2-(x-4)^2=0\)
\(⇔(3x-20)(x-12)=0\)
\(⇔\left[\begin{array}{} 3x-20=0\\ x-12=0 \end{array}\right.\)\(⇔\left[\begin{array}{} x=\frac{20}{3}\\ x=12 \end{array}\right.\)
(Sửa đề 2) \((x^2-16)^2-(x-4)^2=0\)
\(⇔(x^2-x-12)(x^2+x-20)=0\)
\(⇔(x-4)^2(x+3)(x+5)=0\)
\(⇔\left[\begin{array}{} (x-4)^2=0\\\ x+3=0\\ x+5=0 \end{array}\right.\)\(⇔\left[\begin{array}{} x=4\\\ x=-3\\ x=-5 \end{array}\right.\)
AD
1
29 tháng 10 2023
a:
ĐKXĐ: \(x^2+3x>=0\)
=>x(x+3)>=0
=>\(\left[{}\begin{matrix}x>=0\\x< =-3\end{matrix}\right.\)
\(\sqrt{16}-\sqrt{x^2+3x}=0\)
=>\(\sqrt{x^2+3x}=\sqrt{16}\)
=>x^2+3x=16
=>x^2+3x-16=0
\(\text{Δ}=3^2-4\cdot1\cdot\left(-16\right)=9+64=73>0\)
Do đó: Phương trình có 2 nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-3-\sqrt{73}}{2}\\x_2=\dfrac{-3+\sqrt{73}}{2}\end{matrix}\right.\)
b:
ĐKXĐ: \(x\in R\)
\(3x-1-\sqrt{4x^2-12x+9}=0\)
=>\(\sqrt{\left(2x-3\right)^2}=3x-1\)
=>\(\left\{{}\begin{matrix}3x-1>=0\\\left(3x-1\right)^2=\left(2x-3\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{1}{3}\\\left(3x-1-2x+3\right)\left(3x-1+2x-3\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{1}{3}\\\left(x+2\right)\left(5x-4\right)=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\left(loại\right)\\x=\dfrac{4}{5}\left(nhận\right)\end{matrix}\right.\)
c:
ĐKXĐ: \(\left\{{}\begin{matrix}x^2-6x+8>=0\\2x^2-10x+11>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>=4\\x< =2\end{matrix}\right.\\\left[{}\begin{matrix}x< =\dfrac{5-\sqrt{3}}{2}\\x>=\dfrac{5+\sqrt{3}}{2}\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x< =\dfrac{5-\sqrt{3}}{2}\\x>=4\end{matrix}\right.\)
\(\sqrt{2x^2-10x+11}=\sqrt{x^2-6x+8}\)
\(\Leftrightarrow2x^2-10x+11=x^2-6x+8\)
=>\(x^2-4x+3=0\)
=>(x-1)(x-3)=0
=>x=3(loại) hoặc x=1(nhận)
PM
1
10 tháng 8 2017
\(\frac{x^2-2x+1}{x^2-6x+9}=0\)ĐKXĐ: \(x\ne3\)
\(\Leftrightarrow x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x-1=0\)
\(\Leftrightarrow x=1\)( thỏa mãn ĐKXĐ)
vậy phương trình có tập nghiệm là: S={1}
30 tháng 7 2021
1)(x2-4x+16)(x+4)-x(x+1)(x+2)+3x2=0
\(\Rightarrow\)(x3+64)-x(x2+2x+x+2)+3x2=0
\(\Rightarrow\)x3+64-x3-2x2-x2-2x+3x2=0
\(\Rightarrow\)-2x+64=0
\(\Rightarrow\)-2x=-64
\(\Rightarrow\)x=\(\dfrac{-64}{-2}\)
\(\Rightarrow x=32\)
30 tháng 7 2021
2)(8x+2)(1-3x)+(6x-1)(4x-10)=-50
\(\Rightarrow\)8x-24x2+2-6x+24x2-60x-4x+10=50
\(\Rightarrow\)-62x+12=50
\(\Rightarrow\)-62x=50-12
\(\Rightarrow\)-62x=38
\(\Rightarrow\)x=\(-\dfrac{38}{62}=-\dfrac{19}{31}\)
PV
2
DN
23 tháng 3 2016
a.x2+6x+9>0
(x+3)2>0
Vậy đẳng thức trên đúng
b. x2+6x+10>1
x2+6x+9+1>1
(x+3)2>0
Vậy đẳng thúc trên đúng
23 tháng 3 2016
a)\(x^2+6x+9\)
\(\Rightarrow\left(x^2+2.2x.3+3^2\right)\)
\(\Rightarrow\left(x+3\right)^2>0\)
b)\(x^2+6x+10\)
\(\left(x^2+2.2x.3+3^2\right)+1\)
\(\Rightarrow\left(x+3\right)^2+1>1\left(vì\left(x+3\right)^2>0\right)\)
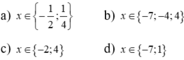
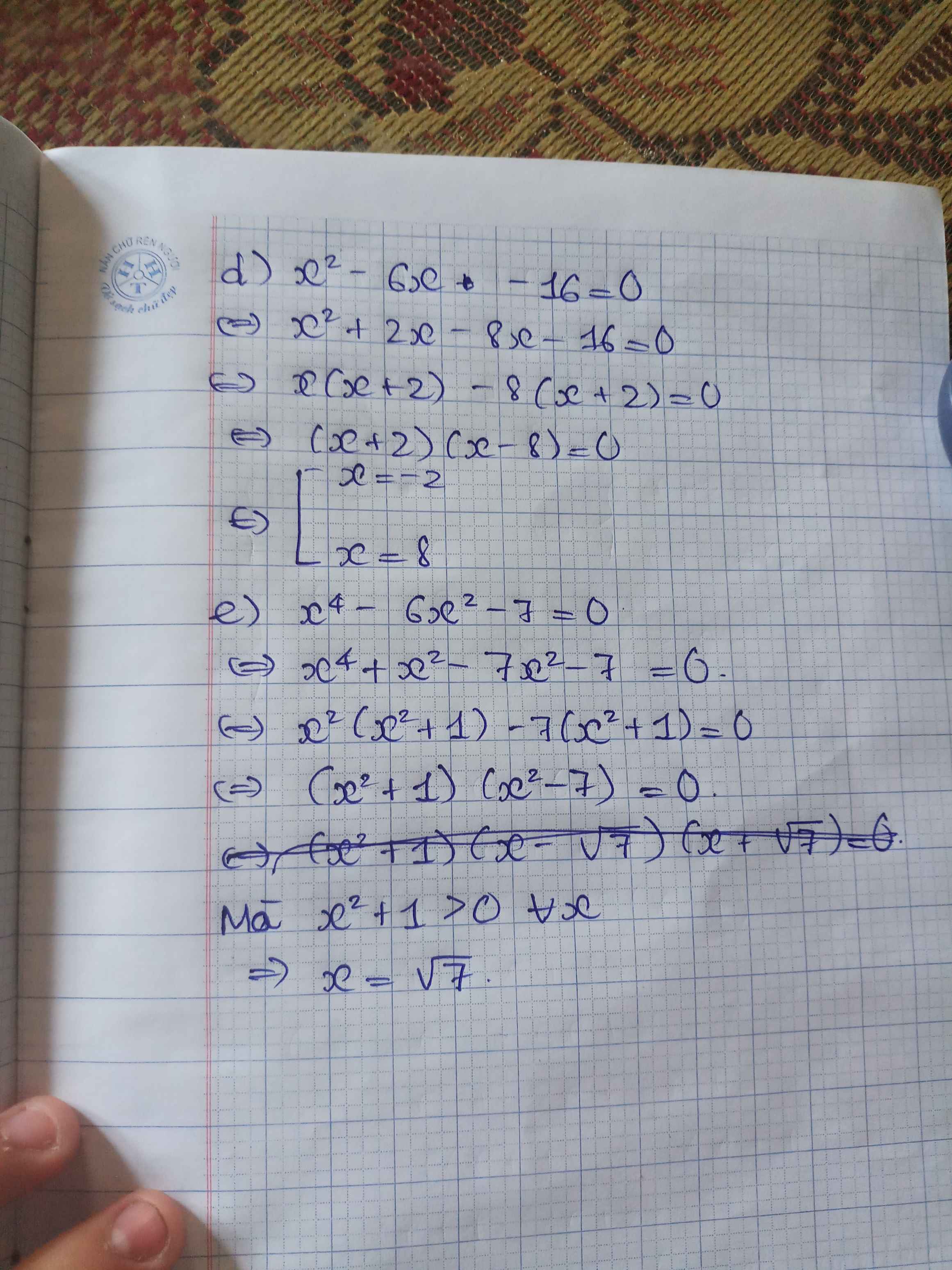
\(x^2-6x+9-16=0\)
\(\Leftrightarrow\left(x-3\right)^2=16\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=4\\x-3=-4\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=7\\x=-1\end{cases}}\)