PM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 8 2021
b)x2-2x+1=4
⇔(x-1)2=4
\(\Leftrightarrow\left[{}\begin{matrix}x-1=2\\x-1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
c)x2-4x+4=9
⇔ (x-2)2=9
\(\Leftrightarrow\left[{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
d)4x2-4x+1=4
⇔ (2x-1)2=4
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=4\\2x-1=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=\dfrac{-3}{2}\end{matrix}\right.\)
e)x2-2x-8=0
⇔ x2-4x+2x-8=0
⇔ x(x-4)+2(x-4)=0
⇔(x-4)(x+2)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
f)9x2-6x-8=0
⇔ 9x2-12x+6x-8=0
⇔ 3x(3x-4)+2(3x-4)=0
⇔ (3x-4)(3x+2)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=\dfrac{-2}{3}\end{matrix}\right.\)
L
1
PV
2
DN
23 tháng 3 2016
a.x2+6x+9>0
(x+3)2>0
Vậy đẳng thức trên đúng
b. x2+6x+10>1
x2+6x+9+1>1
(x+3)2>0
Vậy đẳng thúc trên đúng
23 tháng 3 2016
a)\(x^2+6x+9\)
\(\Rightarrow\left(x^2+2.2x.3+3^2\right)\)
\(\Rightarrow\left(x+3\right)^2>0\)
b)\(x^2+6x+10\)
\(\left(x^2+2.2x.3+3^2\right)+1\)
\(\Rightarrow\left(x+3\right)^2+1>1\left(vì\left(x+3\right)^2>0\right)\)
25 tháng 3 2020
Bài 1:
a) (3x - 2)(4x + 5) = 0
<=> 3x - 2 = 0 hoặc 4x + 5 = 0
<=> 3x = 2 hoặc 4x = -5
<=> x = 2/3 hoặc x = -5/4
b) (2,3x - 6,9)(0,1x + 2) = 0
<=> 2,3x - 6,9 = 0 hoặc 0,1x + 2 = 0
<=> 2,3x = 6,9 hoặc 0,1x = -2
<=> x = 3 hoặc x = -20
c) (4x + 2)(x^2 + 1) = 0
<=> 4x + 2 = 0 hoặc x^2 + 1 # 0
<=> 4x = -2
<=> x = -2/4 = -1/2
d) (2x + 7)(x - 5)(5x + 1) = 0
<=> 2x + 7 = 0 hoặc x - 5 = 0 hoặc 5x + 1 = 0
<=> 2x = -7 hoặc x = 5 hoặc 5x = -1
<=> x = -7/2 hoặc x = 5 hoặc x = -1/5
H9
HT.Phong (9A5)
CTVHS
12 tháng 8 2023
\(M=\left(x+3\right)\left(x^2-3x+9\right)-\left(3-2x\right)\left(4x^2+6x+9\right)\)
\(M=\left(x^3+3^3\right)-\left[3^3-\left(2x\right)^3\right]\)
\(M=x^3+27-27+8x^3\)
\(M=9x^3\)
Thay x=20 vào M ta có:
\(M=9\cdot20^3=72000\)
Vậy: ...
\(N=\left(x-2y\right)\left(x^2+2xy+4y^2\right)+16y^3\)
\(N=x^3-\left(2y\right)^3+16y^3\)
\(N=x^3-8y^3+16y^3\)
\(N=x^3+8y^3\)
\(N=\left(x+2y\right)\left(x^2-2xy+4y^2\right)\)
Thay \(x+2y=0\) vào N ta có:
\(N=0\cdot\left(x^2-2xy+4y^2\right)=0\)
Vậy: ...
5 tháng 7 2019
3x2 + 2x - 1 = 0
=> 3x2 + 3x - x - 1 = 0
=> 3x(x + 1) - (x + 1) = 0
=> (3x - 1)(x + 1) = 0
=> \(\orbr{\begin{cases}3x-1=0\\x+1=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=\frac{1}{3}\\x=-1\end{cases}}\)
x2 - 5x + 6 = 0
=> x2 - 2x - 3x + 6 = 0
=> x(x - 2) - 3(x - 2) = 0
=> (x - 3)(x - 2) = 0
=> \(\orbr{\begin{cases}x-3=0\\x-2=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=3\\x=2\end{cases}}\)
3x2 + 7x + 2 = 0
=> 3x2 + 6x + x + 2 = 0
=> 3x(x + 2) + (x + 2) = 0
=> (3x + 1)(x + 2) = 0
=> \(\orbr{\begin{cases}3x+1=0\\x+2=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=-\frac{1}{3}\\x=-2\end{cases}}\)
5 tháng 7 2019
1, \(3x^2+2x-1=0\Leftrightarrow3x^2+3x-x-1=0\)
\(\Leftrightarrow3x\left(x+1\right)-\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\3x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=\frac{1}{3}\end{cases}}}\)
2, \(x^2-5x+6=0\Leftrightarrow x^2-2x-3x+6=0\)
\(\Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}}\)
3, \(3x^2+7x+2=0\Leftrightarrow3x^2+6x+x+2=0\)
\(\Leftrightarrow3x\left(x+2\right)+\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\3x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=-\frac{1}{3}\end{cases}}}\)
9 tháng 8 2021
a)4x2-9=0
⇔ (2x-3)(2x+3)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
b)(x+5)2-(x-1)2=0
⇔ (x+5-x+1)(x+5+x-1)=0
⇔ 12(x+2)=0
⇔ x=-2
c)x2-6x-7=0
⇔ x2-7x+x-7=0
⇔ x(x-7)+(x-7)=0
⇔ (x-7)(x+1)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=7\\x=-1\end{matrix}\right.\)
d)(x+1)2-(2x-1)2=0
⇔ (x+1-2x+1)(x+1+2x-1)=0
⇔3x(2-x)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
HN
9 tháng 8 2021
a, 4x2 - 9 = 0
<=> 4x2 = 9
<=> x2 = \(\dfrac{9}{4}\) => x = \(\sqrt{\dfrac{9}{4}}\)
b, (x + 5 )2 - ( x - 1 )2 = 0
<=> ( x+5-x+1 )(x+5+x-1) = 0
<=> 6(2x+4) = 0
<=> 12x+24=0
<=> 12x = -24
<=> x = -2
c, x2-6x-7=0
<=> x2+x-7x-7=0
<=> x(x+1)-7(x+1)=0
<=> (x-7)(x+1)=0
=> x+7=0 hoặc x+1=0
+ x-7=0 => x=7
+ x+1=0 => x=-1
d, \(\left(x+1\right)^2-\left(2x-1\right)^2=0\)
<=> \(\left(x+1-2x+1\right)\left(x+1+2x-1\right)=0\)
<=> (-x+2).3x=0
=> x=0 hoặc (-x+2).3=0
+ (-x+2).3=0 => -3x+6=0 => x=-2
PN
15 tháng 5 2021
\(|x-6|=-5x+9\)
Xét \(x\ge6\)thì \(pt< =>x-6=-5x+9\)
\(< =>x-6+5x-9=0\)
\(< =>6x-15=0\)
\(< =>x=\frac{15}{6}\)(ktm)
Xét \(x< 6\)thì \(pt< =>x-6=5x-9\)
\(< =>4x-9+6=0\)
\(< =>4x-3=0< =>x=\frac{3}{4}\)(tm)
Vậy ...
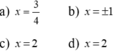
\(\frac{x^2-2x+1}{x^2-6x+9}=0\)ĐKXĐ: \(x\ne3\)
\(\Leftrightarrow x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x-1=0\)
\(\Leftrightarrow x=1\)( thỏa mãn ĐKXĐ)
vậy phương trình có tập nghiệm là: S={1}