Gọi (I;r) là đường tròn nội tiếp \(\Delta ABC\) vuông tại A đường cao AH biết AB = 20cm, AC = 15cm.
a, Tính bán kính r.
b, Tính khoảng cách từ I đến AH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1
a/ AB // DI
Mà AM thuộc tia AB => AM // DI (1)
=> Tứ giác AIDM là hình thang
E là trung điểm của AD (gt) => ED = EA
Xét △EDI và △EAM có:
- Góc DEI = Góc AEM (đối đỉnh)
- ED = EA (cmt)
- Góc EDI = Góc EAM (slt)
=> △EDI = △EAM (g.c.g)
=> AM = DI (2)
Từ (1) và (2). Vậy: Tứ giác AIDM là hình bình hành (đpcm)
b/ Chứng minh tương tự câu a
c/ Hình bình hành BICN có: BN = IC = CD/2 (I là trung điểm của CD)
Hình bình hành AIDM có: MA = ID = CD/2 (I là trung điểm của CD)
=> BN = MA (3)
Mặt khác ta có: H là trung điểm của AB (gt) hay HA = HB (4)
Từ (3) và (4) suy ra: BN + HA = HB + MA
Hay: HM = HN
Hay: H là trung điểm của MN (đpcm
Bài 2: Đề sai nên không thể giải

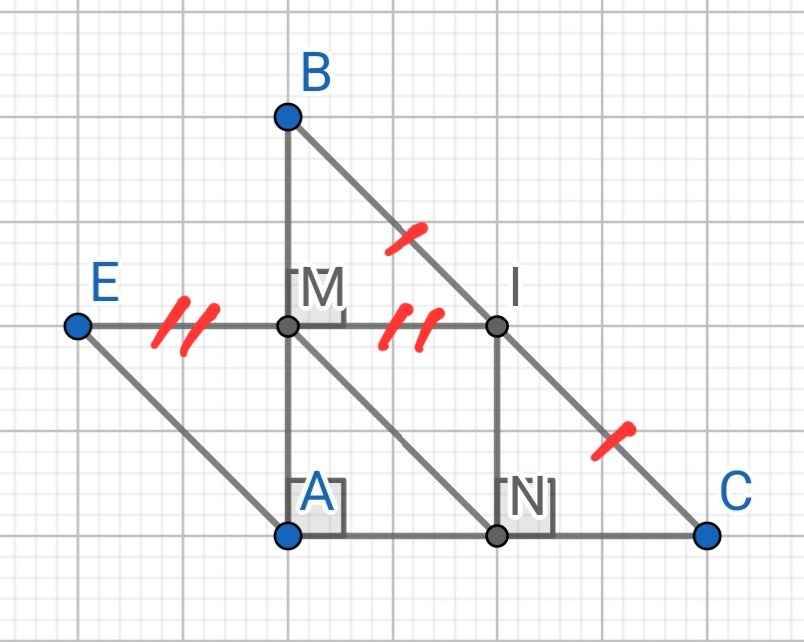
a) Do IM ⊥ AB (gt)
⇒ IM //AC
Mà I là trung điểm BC
⇒ M là trung điểm AB
⇒ IM là đường trung bình của ∆ABC
⇒ IM = AC/2
Do IN ⊥ AC (gt)
IN // AB
Mà I là trung điểm BC
⇒ N là trung điểm AC
⇒ AN = AC/2
⇒ IM = AC/2 = AN
Do IM // AC
⇒ IM // AN
Do M là trung điểm AB (cmt)
⇒ AM = IM = AB/2
Xét tứ giác AMIN có:
IM // AN (cmt)
IM = AN (cmt)
⇒ AMIN là hình bình hành
Mà ∠MAN = 90⁰ (∆ABC vuông tại A)
⇒ AMIN là hình chữ nhật
Lại có AM = IM (cmt)
⇒ AMIN là hình vuông
b) Do M là trung điểm AB (cmt)
N là trung điểm AC (cmt)
⇒ MN là đường trung bình của ∆ABC
⇒ MN // BC
c) Do E đối xứng với I qua M (gt)
⇒ ME = IM
⇒ ME = AN
Do IM // AN (cmt)
⇒ ME // AN
Xét tứ giác AEMN có:
ME // AN (cmt)
ME = AN (cmt)
⇒ AEMN là hình bình hành

IB=8/4=2cm
=>IA=6cm
=>AD=2*6=12cm
EI=căn AI*IB=2*căn 3(cm)
=>EF=4*căn 3(cm)
Xét tứ giác AEDF có
I là trung điểm chung của EF và AD
EF vuông góc AD
=>AEDF là hình thoi
=>S AEDF=1/2*AD*EF=1/2*4*căn 3*12=24*căn 3(cm2)

Tham khảo nhé bạn:![]()
Tên gọi cuối thế kỉ XĨ đầu thế kỉ XX là:
Anh: Chủ nghĩa đế quốc thực dân
Pháp: Chủ nghĩa đế quốc cho vay lãi
Đức:Chủ nghĩ quân phiệt hiếu chiến
Mĩ: chủ nghĩa đế quốc Các-tơ-rốt
![]()

Dựa và ý a)
Có \(\dfrac{IM}{AC}=\dfrac{BI}{BC}=\dfrac{1}{2}\) ( định lý thales )
mà IM // AC ( cùng vuông góc với AB )
\(\Rightarrow\) IM là đường trung bình của tam giác ABC mà I là trung điểm của BC
\(\Rightarrow\) M là trung điểm của AB
Lại có \(\dfrac{IN}{AB}=\dfrac{IC}{CB}=\dfrac{1}{2}\) ( đly thales )
mà IN // AB ( cùng vuông góc với AC )
\(\Rightarrow\) IN là đường tb của tam giác ABC
mà I là trung điểm của BC nên N là trung điểm của AC
Có M và N lần lượt là trung điểm của AB và AC
\(\Rightarrow\) MN là đường trung bình của tam giác ABC
Suy ra MN // BC

Bài 1:
Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
I là trung điểm của GB
K là trung điểm của GC
Do đó: IK là đường trung bình của ΔGBC
Suy ra: IK//BC và \(IK=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra DE//IK và DE=IK