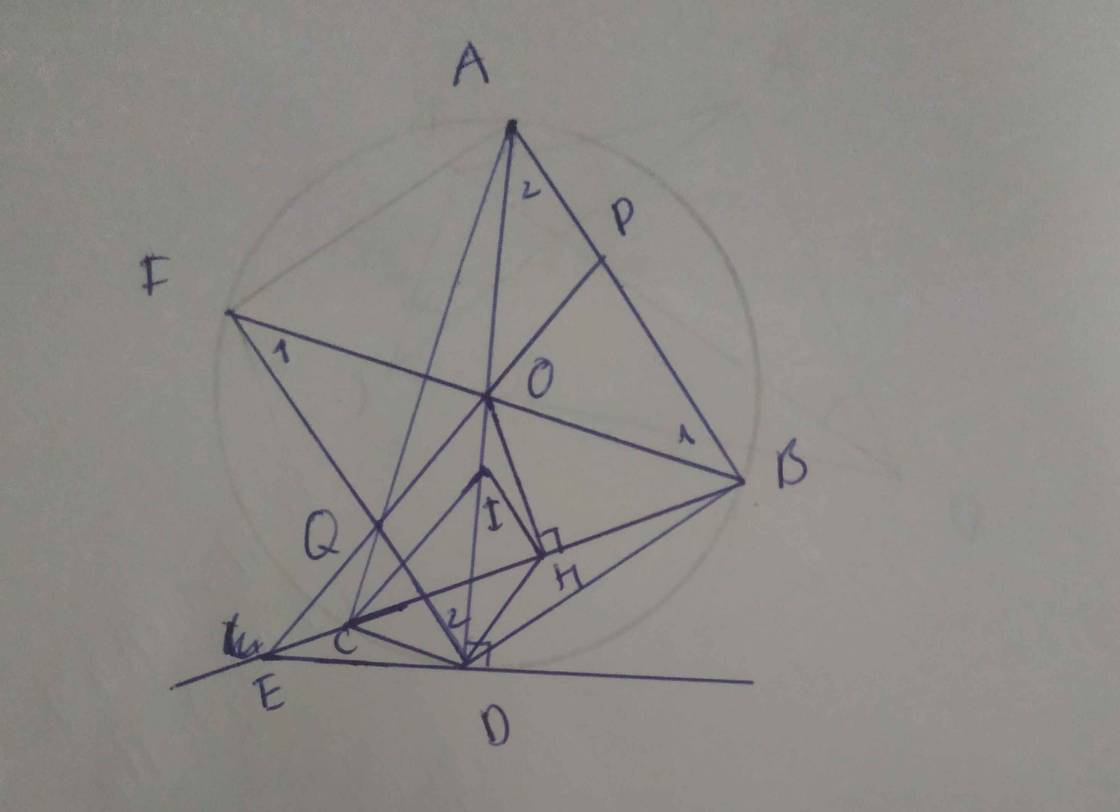
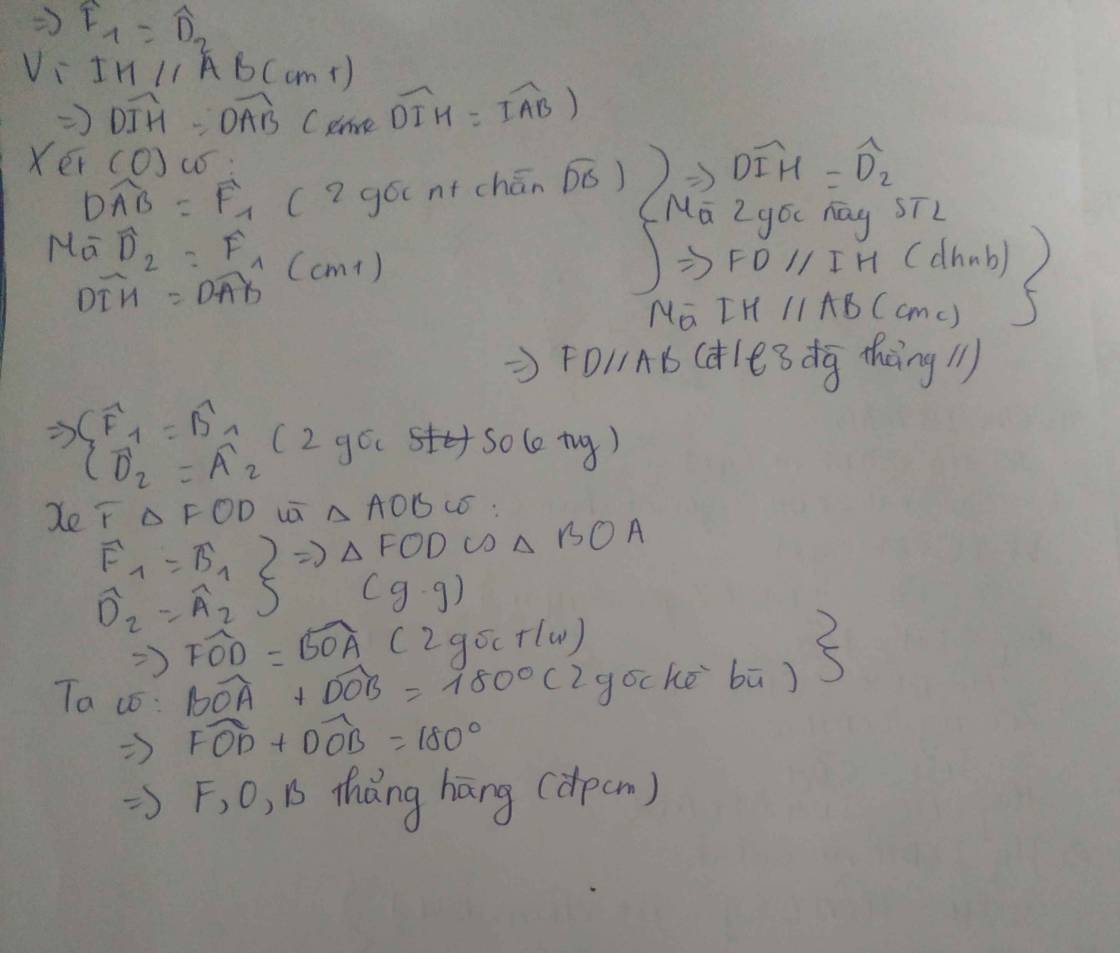Cho tam giác ABC vuông tại A ngoại tiếp đường tròn (I,r). C/minh: \(r=\frac{AB+AC-BC}{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


r r r A B C M N P I
Gọi M, N, P lần lượt là tiếp điểm của (I;r) với AB; BC; AC
Có: \(AB+AC-BC=AM+MB-BN-NC+CP+PA\)
Mà \(MB=BN\); \(NC=CP\); \(AM=PA\)
=> \(AB+AC-BC=2AM\)
Xét tứ giác MIPA có 3 góc vuông => MIPA là hình chữ nhật
=> \(AM=IP=r\)
=> \(r=AM=\frac{AB+AC-BC}{2}\)


Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC.
Ta có: BC = 2R
Giả sử đường tròn (O) tiếp với AB tại D, AC tại E và BC tại F
Theo kết quả câu a) bài 58, ta có ADOE là hình vuông.
Suy ra: AD = AE = EO = OD = r
Theo tính chất hai tiếp tuyến cắt nhau ta có:
AD = AE
BD = BF
CE = CF
Ta có: 2R + 2r = BF + FC + AD + AE
= (BD + AD) + (AE + CE)
= AB + AC
Vậy AB = AC = 2(R + r)

Tìm ba phân số khác nhau biết phân số thứ nhất và phân số thứ hai là 7/8,tổng của phân số thứ hai và phân số thứ ba là 8/7,tổng của phân số thứ nhất và phân số thứ ba là 8/9

B F C O D A E
Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC.
Ta có: BC = 2R
Giả sử đường tròn (O) tiếp với AB tại D, AC tại E và BC tại F
Theo kết quả câu a) bài 58, ta có ADOE là hình vuông.
Suy ra: AD = AE = EO = OD = r
Theo tính chất hai tiếp tuyến cắt nhau ta có:
AD = AE
BD = BF
CE = CF
Ta có: 2R + 2r = BF + FC + AD + AE
= ( BD + AD ) + ( AE + CE )
= AB + AC
Vậy AB = AC = 2 ( R + r )

ta có : BC = 2R ; AD = AE = r
nên 2R + r = BC + (AE + AD) = (BF + FC) + (AE + AD)
= (DB + EC) + (AE + AD) = (AD + DB) + (AE + EC)
= AB + AC ( đpcm)