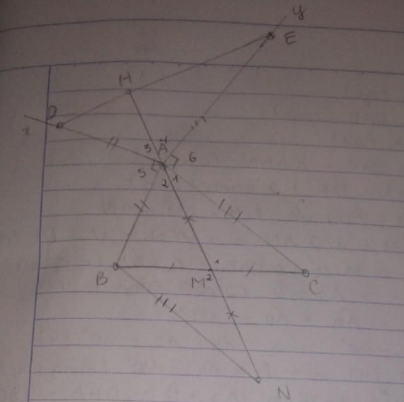
Cho tam giác có RS = RT. Trên nửa mặt phẳng bờ RS không chứa điểm T, vẽ tia Ry vuông góc vs RS. Trên nửa mặt phẳng bờ là RT ko chứa S vẽ tia Rx vuông góc vs RT. Trêm Rx, Ry lần lượt lấy M, N sao cho RM = RN. Chứng minh:
a) góc SRx = góc TRy
b) SM = TN.

a) Có: \(Ry\perp RS\Rightarrow\widehat{SRy}=90^o\\ Rx\perp RT\Rightarrow\widehat{TRx}=90^o\)
Có: \(\widehat{SRx}=\widehat{SRT}+\widehat{TRx}\\ \widehat{TRy}=\widehat{SRT}+\widehat{SRy}\)
Mà \(\widehat{TRx}=\widehat{SRy}\left(=90^o\right)\)
\(\Rightarrow\widehat{SRx}=\widehat{TRy}\)
b) Xét ΔSRM và ΔTRN có:
\(RS=RT\left(gt\right)\\ \widehat{SRx}=\widehat{TRy}\left(cmt\right)\\ RM=RN\left(gt\right)\)
\(\Rightarrow\Delta SRM=\Delta TRN\left(c.g.c\right)\\ \Rightarrow SM=TN\left(\text{2 cạnh tương ứng}\right)\)
loz